Tarjan DFS

Algorithm

May 20, 2023

本文资料来源于¹²

Tarjan 其实是老朋友了，之前介绍过的斐波那契堆（1986），他就是它的两位作者之一，现在是要介绍他早期（1972、1973）发表的通过图上 DFS 来线性时间解决³：

在无向图上划分双联通分量
查找强连通分量

其中一些概念也是（可能）后续一些基于 DFS 的算法的基础。

深度优先遍历

对一个连通无向（简单）图，如下所示：

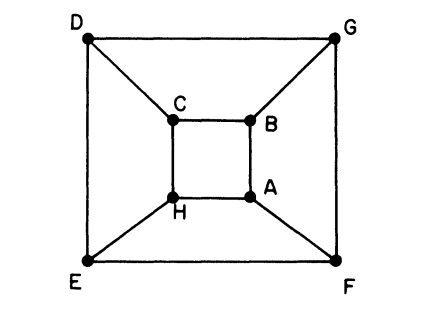
（默认按照字母顺序）进行深度优先地图上遍历：

\[\begin{array}{l} \text{A}\rightarrow \text{B}\rightarrow \text{C}\rightarrow \text{D}\rightarrow &\text{E}\rightarrow &\text{F}\curvearrowright \text{A}\\ && \text{F}\rightarrow&\text{G}\curvearrowright\text{D}\\ &&&\text{G}\curvearrowright\text{B}\\ &\text{E}\rightarrow&\text{H}\curvearrowright \text{A}\\ &&\text{H}\curvearrowright \text{C} \end{array}\]

得到一个包含一棵生成树 $\text{T}$ 的有向图 $\text{P}$，并按照访问顺序，从 $1$ 开始给 $\text{P}$ 上每个点编号：

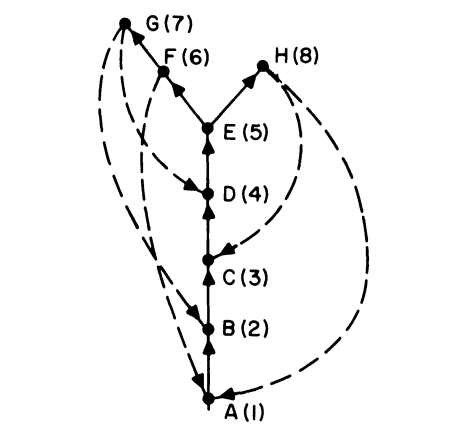
后面的算法都以 DFS 构建的有向图 $\text{P}$ 为基础，观察它的回溯边的情况。

回溯边，可以分为两种情况：

如上图所示，从某个点回到它的一个祖先节点的一条边，比如 $\text{G}\curvearrowright\text{D}$ ，可以叫它叶边（frond）；
上图没有的，从某个点回到不是它祖先节点（但是也比它更早访问到）的一条边，比如$\text{G}\curvearrowright\text{H}$ ，可以叫它横叉边（cross link）

如果 $\text{P}$ 的所有回溯边都是叶边，那么可以称它为棕榈树（palm tree）⁴。

可以发现，在任意无向连通图上做 DFS ，构建的有向图 $\text{P}$ 一定是棕榈树；反之任意棕榈树 $\text{P}$ 一定可以由一个它的无向图版本做 DFS 得到。

换言之，无向图 DFS，不存在横叉边。运用反证法：因为是无向图，如果存在横叉边，那么它就应该作为 DFS 过程中生成树上的一条边，而不是回溯边。

根据某个点的所有后代的回溯边所能到达的编号最小的点，引出一个关键概念 – LOWPT⁵：

$\text{lowpt}(v)$ 定义为从 $v$ 出发，经过零个或更多的树弧，和最多一条回溯边，所能到达的编号最小的点（我们不妨用 $\text{index}(v)$ 表示 $v$ 点的编号）。

双联通分量

有了前面的知识铺垫，我们可以通过 DFS ，首先来解决在无向图上的双连通分量（biconnected component, bcc）的划分问题，而在具体讨论之前，有必要先理清下概念：

概念

2-连通图

读作 $2$ 点连通图，是 $k$ 点连通图的一个实例，也就是一个连通图里有只有删除两个点才能导致图不连通。

双连通图

双联通图（biconnected graph）大多数情况下和 2-连通图（2-connected graph）是等价的，只在一个例外，就是只包含一条边的图仍然是双联通图，但一般不被视为 2-连通图⁶⁷。

双连通图之所以有这么个特殊例外，就是为了方便把图按双连通分量进行划分，对剩下的散碎边，每条边都可以视为一个最小的双连通分量。

算法

划分双连通分量的关键在于寻找分量之间的衔接点（articulation point）⁸。

衔接点可以利用计算的 $\text{lowpt}$ 寻找：在 DFS 构建的有向图 $\text{P}$ 上，如果一个点的 $\text{lowpt}$ 不低于它的父节点的编号，那么它的父节点就是一个衔接点。

比如，对于下图

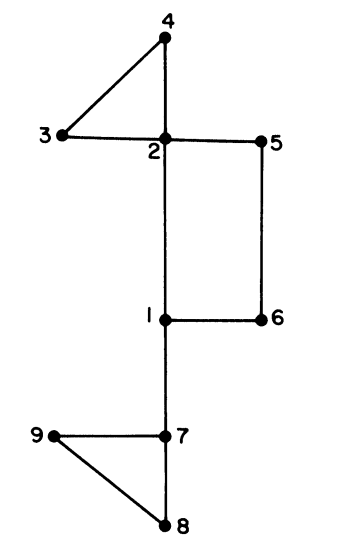
DFS 构建的有向图：

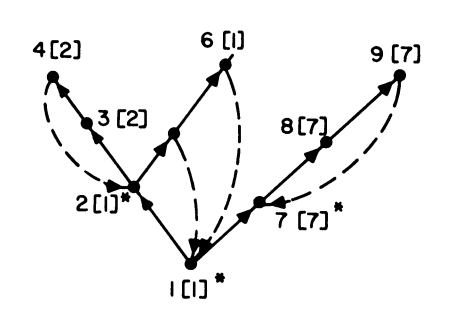
上图 G 点的 $\text{lowpt}(3)=2=\text{index}(2)$ ，因此 $3$ 的父节点 $2$ 就是一个衔接点，如果此时把之前遍历过程中入栈的边 $2\rightarrow 3$ ，$3\rightarrow 4$，$4\rightarrow2$ 从栈顶依次弹出，那么就收集了一个双联通分量的划分。

最终如下图：

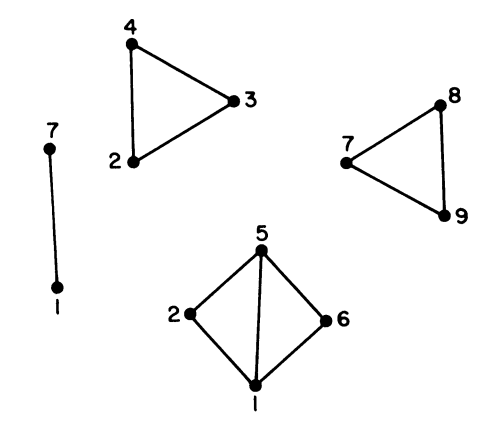
伪代码有些吃力不讨好，不如直接看实现

实现

源代码

数据结构

每个点要保存它的 DFS 编号和 $\text{lowpt}$ ，用 Option 类型指示该点是否被访问。

#[derive(Default, Clone, Copy)]
struct DFSMeta {
    index: Option<usize>,
    lowpt: usize,
}

整体过程

把图中每个点从 $1$ 开始编号，使用一个数组保存它们的元信息。

对图上每个点遍历，如果该点没有被标记过，就执行 DFS 子过程，这么做是考虑到给定的图不一定是连通的，需要在不同分量上分别进行 DFS。

pub fn bcc_tarjan(g: &Graph) -> Vec<Vec<(usize, usize)>> {
    let mut bccs = Vec::new();

    if g.e.is_empty() {
        return bccs;
    }

    let mut stack = vec![];
    let mut index = 0;

    let max_v = g.vertexs().max().unwrap();

    let mut vertexs = vec![DFSMeta::default(); max_v + 1];

    for u in g.vertexs() {
        if vertexs[u].index.is_none() {
            dfs_bcc(
                g,
                u,
                max_v + 1,
                &mut bccs,
                &mut stack,
                &mut index,
                &mut vertexs,
            )
        }
    }

    bccs
}

DFS 子过程

fn dfs_bcc(
    g: &Graph,
    u: usize,
    p: usize,
    mut bccs: &mut Vec<Vec<(usize, usize)>>,
    stack: &mut Vec<(usize, usize)>,
    index: &mut usize,
    vertexs: &mut Vec<DFSMeta>,
) {
    *index += 1;

    vertexs[u] = DFSMeta {
        index: Some(*index),
        lowpt: *index,
    };

    for v in get!(g.e => u => vec![]) {
        if vertexs[v].index.is_none() {
            stack.push((u, v));
            dfs_bcc(g, v, u, bccs, stack, index, vertexs);

            if vertexs[v].lowpt < vertexs[u].lowpt {
                vertexs[u].lowpt = vertexs[v].lowpt;
            }

            if vertexs[u].index.unwrap() == vertexs[u].lowpt {
                // u is cut point
                // get biconnected component

                let mut bcc = vec![];

                loop {
                    let (v1, v2) = stack.pop().unwrap();
                    ordered_insert!(
                        &mut bcc,
                        if v1 < v2 { (v1, v2) } else { (v2, v1) }
                    );

                    if v1 == u {
                        break;
                    }
                }

                ordered_insert!(&mut bccs, bcc, |bcc: &Vec<(usize, usize)>| bcc[0]);
            }
        } else if vertexs[v].index < vertexs[u].index && v != p {
            stack.push((u, v));

            if vertexs[v].index.unwrap() < vertexs[u].lowpt {
                vertexs[u].lowpt = vertexs[v].index.unwrap();
            }
        }
    }
}

部分参数解释

p，对于无向（简单）图，需要传一个父节点参数 $p$ 来标记“来边”；
bccs 保存划分出的双连通分量的边集，用边集而不是点集是因为双连通分量之间有点是有交合的（就是衔接点），但是边集是不相交的；
stack 保存 DFS 过程访问过的边，用来发现衔接点后收集新的双连通分量的边；
index 点访问的顺序

过程解释

初始化被访问点的编号 $\text{index}$ 和 $\text{lowpt}$ ，其中 $\text{lowpt}$ 初始化的时候与编号一致。

遍历访问点 $u$ 所有的出边，如果出边的头节点 $v$ 未被编号，就推边入栈，并在 $v$ 上执行 DFS 操作，之后利用 $\text{lowpt}(v)$ 更新 $\text{lowpt}(u)$ ，并检查 $\text{lowpt}(v)$ 是否不小于 $\text{index}(u)$ ⁹，如果是，就收集栈上的边，直到收集完起点为 $u$ 的边¹⁰；

如果 $v$ 已被编号，就用它的编号更新 $\text{lowpt}(u)$ ，当然要排除父节点的情况，避免重复访问同一条边。

另外如果对边集里的边和边集的顺序有要求，那么这个过程还要额外进行一个排序。

ordered_insert

#[macro_export]
macro_rules! ordered_insert {
    ($vec:expr, $x:expr) => { {
        let vec = $vec;
        let x = $x;

        match vec.binary_search(&x) {
            Ok(oldidx) => {
                Some(std::mem::replace(&mut vec[oldidx], x))
            },
            Err(inseridx) => {
                vec.insert(inseridx, x);
                None
            },
        }
    } };
    ($vec:expr, $x:expr, $f:expr) => { {
        let vec = $vec;
        let x = $x;
        let f = $f;

        match vec.binary_search_by_key(&f(&x), f) {
            Ok(oldidx) => {
                Some(std::mem::replace(&mut vec[oldidx], x))
            },
            Err(inseridx) => {
                vec.insert(inseridx, x);
                None
            },
        }
    } };
}

时间复杂度

不考虑对结果的标准化问题，时间复杂度显然为 $O(V)+O(E)$

强连通分量

前面讲了无向图上双连通分量的划分，但对于有向图而言，DFS 将不会是一个简单的棕榈树的结构，因为边的方向是固定的，而不是双向都可以的，但（据作者说：“The more complicated structure which results in this case is still simple enough to prove useful in at least one application.”）

不过不管那些，还可以用一个与上述算法非常相似的过程解决有寻找向图上的强连通分量问题（strong connected component，scc）。

算法

如果从一个点出发，最后又回到了该点，那么这个点就是强连通分量的根节点。也就是说，如果在 $u$ 点的所有出边 DFS 结束后，发现 $\text{index}(u)=\text{lowpt}(u)$ ，那么 $u$ 就是一个强连通分量的根节点，而此时收集栈上所有编号大于 $u$ 的点，就得到了这个强连通分量的点集。

实现

源代码

数据结构

新字段 on_stack 用来指示当前节点是否在栈上，这样相比用单独的哈希集合来维护，有更好的局部性。而之所以要检查节点是否在栈上，后面会解释。

#[derive(Default, Clone, Copy)]
struct DFSMeta {
    index: Option<usize>,
    lowlink: usize,
    on_stack: bool
}

整体过程

和划分 BCC 时一样，区别只在于，使用了点集取代边集，这是因为只需要寻找从 SCC 而不是对图进行划分。

pub fn scc_tarjan(g: &Graph) -> Vec<Vec<usize>> {
    let mut comps = Vec::new();

    if g.e.is_empty() {
        return comps;
    }

    let mut stack = vec![];
    let mut index = 0;

    let max_v = g.vertexs().max().unwrap();

    let mut vertexs = vec![DFSMeta::default(); max_v + 1];

    for u in g.vertexs() {
        if vertexs[u].index.is_none() {
            dfs_scc(g, u, &mut comps, &mut stack, &mut index, &mut vertexs)
        }
    }

    comps
}

DFS子过程

同样类似于划分 BCC ，需要注意得是在 DFS 过程中，由于是有向图，所以要考虑 $u$ 的出边节点 $v$ 不与它在同一 SCC 的情况，判断方法是：如果不在同一 SCC ，那么在 DFS 过程中必然已经划分到其他的 SCC 中去了，因此已经从栈上弹出了，所以只需要检查该点是否还在栈上就可以，这就是 on_stack 字段的作用。

fn dfs_scc(
    g: &Graph,
    u: usize,
    comps: &mut Vec<Vec<usize>>,
    stack: &mut Vec<usize>,
    index: &mut usize,
    vertexs: &mut Vec<DFSMeta>,
) {
    vertexs[u] = DFSMeta {
        index: Some(*index),
        lowlink: *index,
        on_stack: true,
    };

    *index += 1;
    stack.push(u);

    for v in get!(g.e => u => vec![]) {
        if vertexs[v].index.is_none() {
            dfs_scc(g, v, comps, stack, index, vertexs);

            if vertexs[v].lowlink < vertexs[u].lowlink {
                vertexs[u].lowlink = vertexs[v].lowlink;
            }

        } else if vertexs[v].index < vertexs[u].index
        && vertexs[v].on_stack
        {
            if vertexs[v].index.unwrap() < vertexs[u].lowlink {
                vertexs[u].lowlink = vertexs[v].index.unwrap();
            }
        }
    }

    /* start a new scc */

    if vertexs[u].lowlink == vertexs[u].index.unwrap() {
        let mut new_comp = Vec::new();

        while let Some(s) = stack.pop() {
            ordered_insert!(&mut new_comp, s);
            vertexs[s].on_stack = false;

            if s == u {
                break;
            }
        }

        ordered_insert!(comps, new_comp, |x: &Vec<usize>| x[0]);
    }
}

时间复杂度

不考虑对结果的标准化问题，时间复杂度显然为 $O(V)+O(E)$

无向图

显然上述求取有向图上 SCC 的算法也完全适应于求取无向图上的连通分量问题。一般使用并查集（multiset union, disjoint set union, union find, etc.）直接计算的话，每条边需要额外付出并查集的 $O(\text{log}(V))$ 的时间复杂度，表现要差于 Tarjan 算法。

注解

Depth-first search and linear graph algorithms R Tarjan - SIAM journal on computing, 1972 ↩
Algorithm 447: efficient algorithms for graph manipulation J Hopcroft, R Tarjan - Communications of the ACM, 1973 ↩
第二篇论文还提到了在双联通分量上的简单路径划分，但是既缺乏具体解释，流程图也模糊不清，伪代码还是 goto 结构的，令人实在没有时间去看了 ↩
“棕榈树”和“叶边”都是作者在论文¹里起的形象名字 ↩
曾经，在第一篇论文里，作者提出的LOWPT的定义是：“That is, LOWPT(v) is the smallest vertex reachable from v by traversing zero or more tree arcs followed by at most one frond. ”；还提出了另外一个相似的概念 LOWLINK：“That is, LOWLINK (v) is the smallest vertex which is in the same component as v and is reachable by traversing zero or more tree arcs followed by at most one frond or cross-link.” 。这两者的本质上显然是相同的，区别只在于一个是应用在无向图上（划分bcc）所以回溯边只经过叶边，而另一个是应用在有向图上（划分scc）所以回溯边可能经过叶边或者横叉边，至于“在同一个分量里”的说法，只能说是回溯的必然结果，而不是限制。而在第二篇论文里，作者也不再区分，而是统一使用了LOWPT。 ↩
https://en.wikipedia.org/wiki/Biconnected_graph# ↩
当然单点图，也就是不含边的图既不是双连通图也不是2-连通图 ↩
也就是割点（cut point），但是割点有些抽象，我们不会进入那个领域 ↩
这里直接检查了 $\text{lowpt}(u)$ 是否被更新得更小 ↩
注意栈上的顺序与访问的顺序是反向的 ↩