斐波那契堆（Fibonacci Heap）

Fibonacci Heap^{12 3}是一个基于链表结构的，理论时间复杂度很优的堆。

常用于 Dijkstra 最短路径、Prim 最小生成树等贪心算法，使用 push - decrease-key，都是 $O(1)$ 的时间复杂度。

预备知识

二项式树 （Binomial Tree）

秩、阶、度 （rank/order/degree）

$\texttt{order}$ ，通常指允许的最大孩子数量，比如二叉树的 $\texttt{order}$ 为 $2$ ；

$\texttt{degree}$ ，具体某个节点的孩子个数；

$\texttt{rank}$ ，一般指排名，但这里用作 $\texttt{degree}$ 的别名；

以下统一用 $\texttt{rank}$ ，指代孩子个数。

性质与定义

1. 二项树的节点数为 ${\large 2^{\text{rank}}}$ ；

2. 显然单节点树的 $\texttt{rank=0}$ ，而合并两棵单节点树可以得到 $\texttt{rank=1}$ 的树，合并两棵 $\texttt{rank=1}$ 的树可以得到 $\texttt{rank=2}$ 的树，由此可归纳得到 $\texttt{rank=k, (k>0)}$ 可以由两棵 $\texttt{rank=k-1}$ 的树合并得到，这就是二项式树的构造；

3. 特别地，从实现上讲，每次同 $\texttt{rank}$ 的树合并，都是其中一棵作为另一棵的最左子树，这样构造出的二项式树的子树也是二项式树，假设 $\texttt{rank=k} $，而且从左到由的 $\texttt{rank}$ 分别为 $\texttt{k-1, k-2, …, 0} $ 。

二项式堆（Binomial Heap）就是由多棵二项式树构成，每棵树都是小顶堆（Min Heap），并且每棵子树的 $\texttt{rank}$ 独特。

每个二项式堆都可以这样构造出来，二项式堆的结点数 $\texttt{n}$ 的二进制表示的每一位对应一个 $\texttt{rank}$ 数值。

而二项堆里的每棵二项树的孩子构成的森林都可以理解为完全二项堆。

定义

斐波那契堆类似于二项式堆，是一个二项式树的森林，但并不严格要求 $\texttt{rank}$ 独特。

执行 push 操作的时候新节点直接作为单节点的二项式树，插入到根链表中。只有在 pop 操作的时候递归合并同 $\texttt{rank}$ 的树，才得到严格的二项式堆。

数据结构

堆的结构：一个指向森林中最小根的指针，以及其他必要元数据；

树根的存储结构：双头循环链表；

树的结构：经典带反向引用的 child-sibling 链表。

Push 操作

算法

根据定义，直接把单个节点插入到根链表中即可，必要的话更新堆指针。

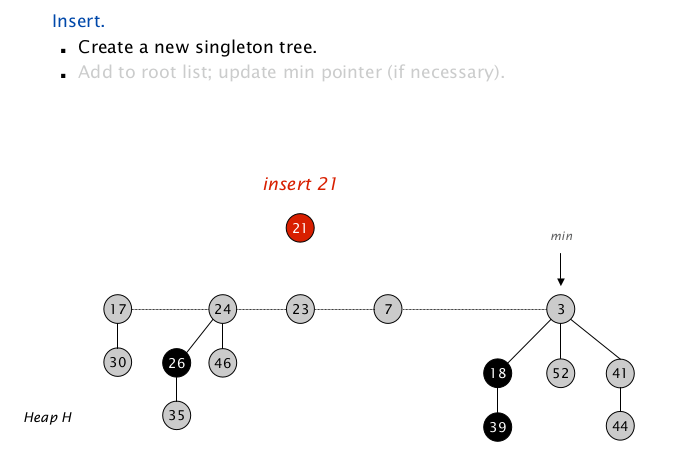
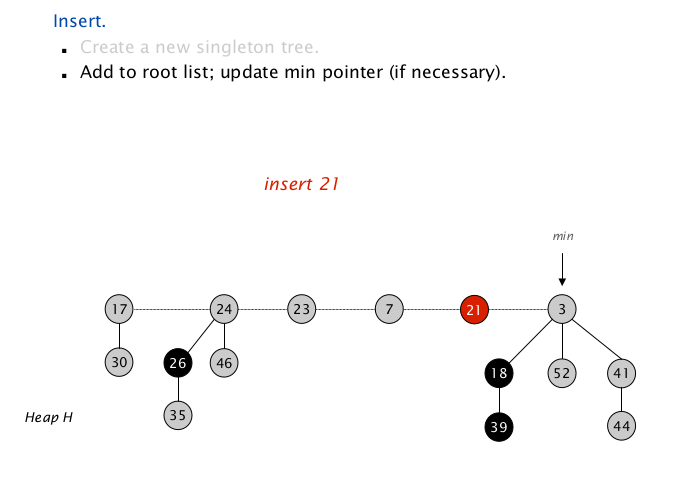
复杂度分析

时间复杂度显然为 $O(1)$ 。

Pop 操作

算法

pop算法分为几步：

1. 把 min 所指向根的树的所有孩子插入到根链表中，然后遍历根列表找到下一个最小根，最后把旧根从根链表中删除；

2. 从更新后的最小根出发，再次遍历根链表，在这个过程中构建 $\texttt{rank => root}$ 的 $\texttt{Map}$ ，当发现新的根的 $\texttt{rank}$ 已在 $\texttt{Map}$ 中存在时，递归地合并同 $\texttt{rank}$ 的树。显然整个过程一遍扫描就可以完成，结果是规整成了一棵严格二项式树

举例来看：

图中黑色节点为标记节点，decrease-min 操作中使用，表示该树失去过孩子

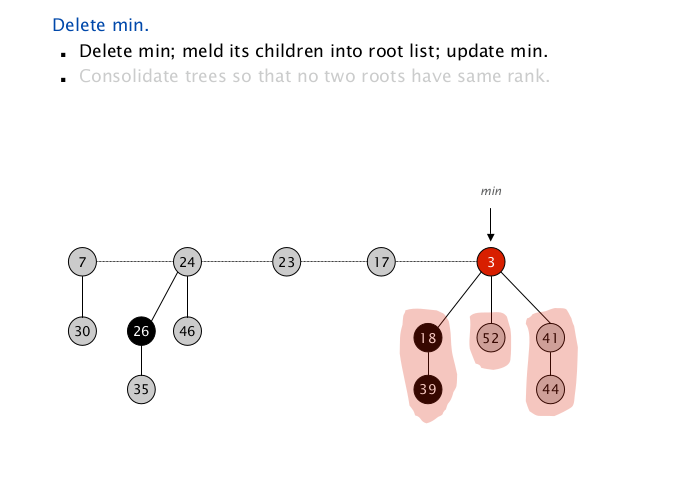
当前最小根指向 $\texttt{node(3)}$，它的孩子有 $\texttt{node(18), node(52), node(41)}$ ；

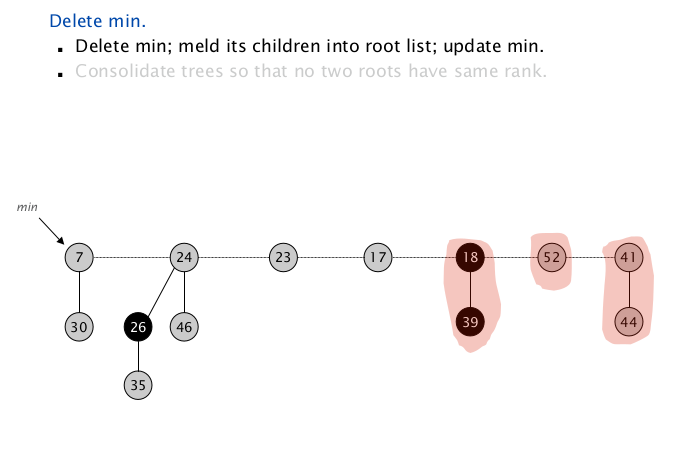
把它的 $3$ 个孩子插入到根链表中，更新最小根为 $7$ ；

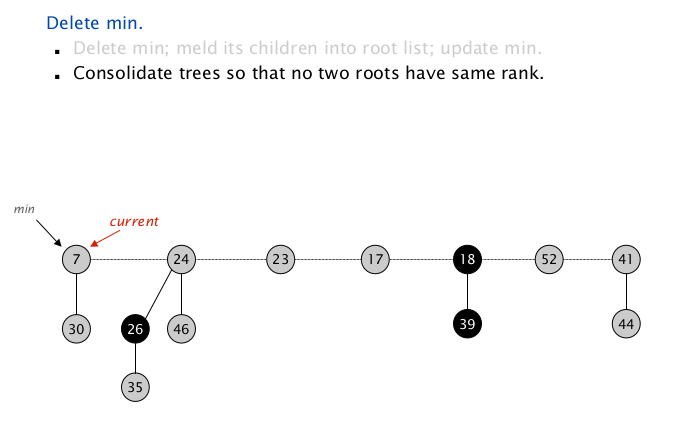
从当前最小根节点开始递归地合并同 $\texttt{rank}$ 的树；

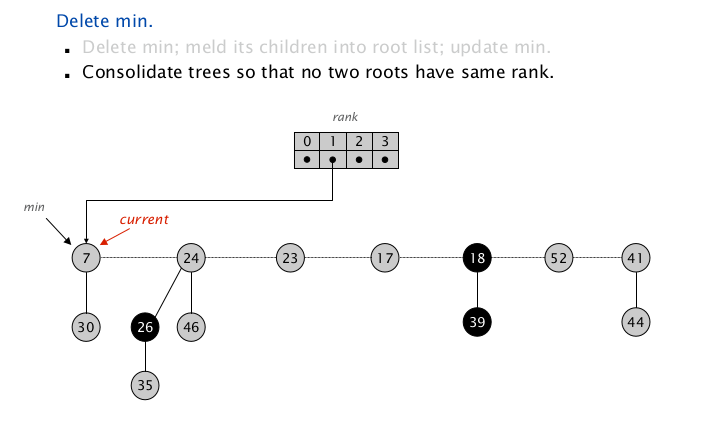
扫描到 $\texttt{node(7)}$ ， $\texttt{rank = 1}$ ，插入当前 $\texttt{rank => root}$ 对儿到 $\texttt{Map}$ 中，继续向下扫描；

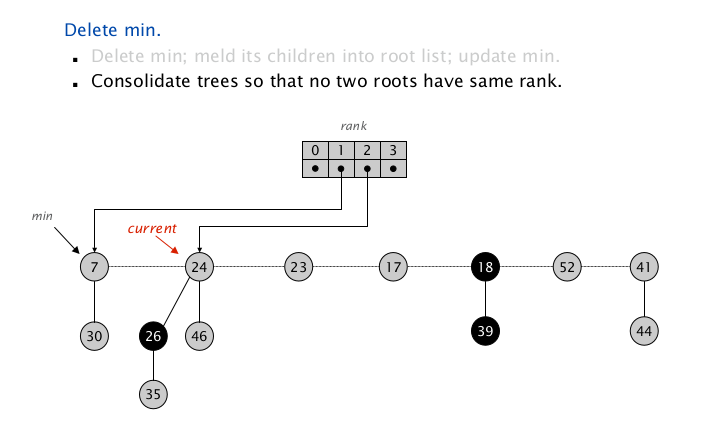
扫描到 $\texttt{node(24)}$ ， $\texttt{rank = 2}$ ，Map中没有同 $\texttt{rank}$ 项，插入当前 $\texttt{rank => root}$ 对儿到 $\texttt{Map}$ 中，继续向下扫描；

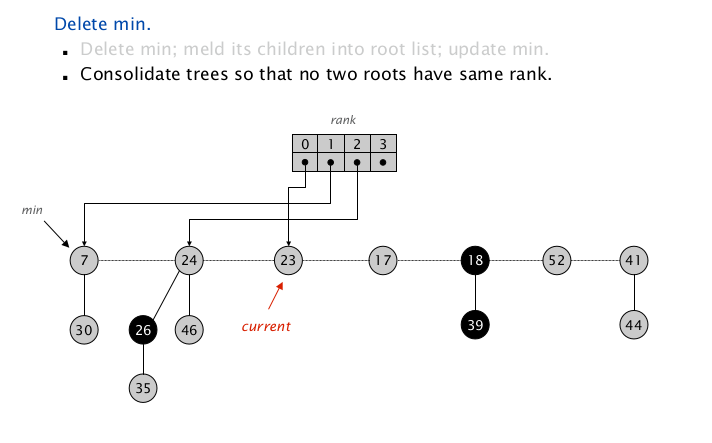
扫描到 $\texttt{node(23)}$ ， $\texttt{rank = 0}$ ，Map中没有同 $\texttt{rank}$ 项，把 $\texttt{0 => node(23)}$ 插入到 $\texttt{Map}$ 中，继续向下扫描；

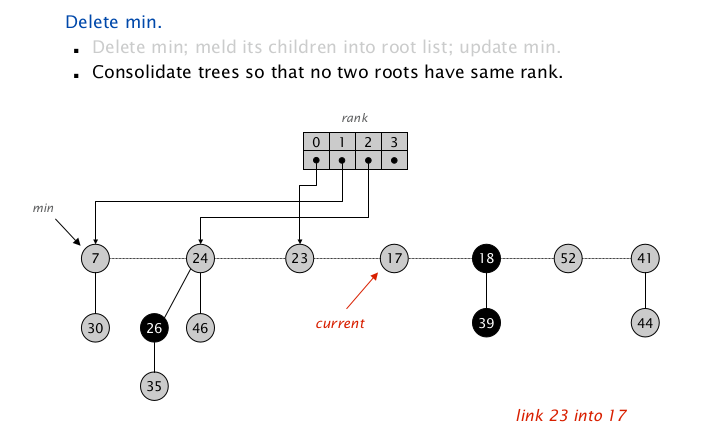
扫描到 $\texttt{node(17)}$ ，$\texttt{rank = 0}$ ，Map中发现同 $\texttt{rank}$ 的 $\texttt{node(23)}$ ，把该项从 $\texttt{Map}$ 取出， 把较大的 $\texttt{node(23)}$ 插入到 $\texttt{node(17)}$ ，检查同 $\texttt{rank}$ 项 显然这个同 rank 树的合并不影响后面没扫描过的根节点；

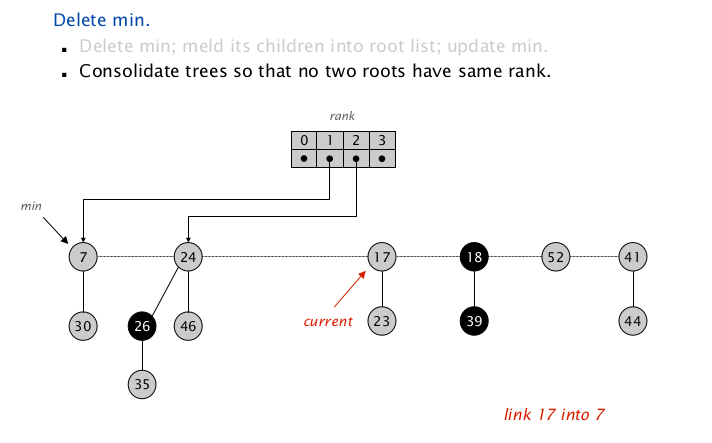
更新后的 $\texttt{17}$ 的 $\texttt{rank += 1}$ ，为 $1$ ，与 $\texttt{node(7)}$ 相同，继续合并，较大的 $\texttt{node(17)}$ 插入到 $\texttt{node(7)}$ ；

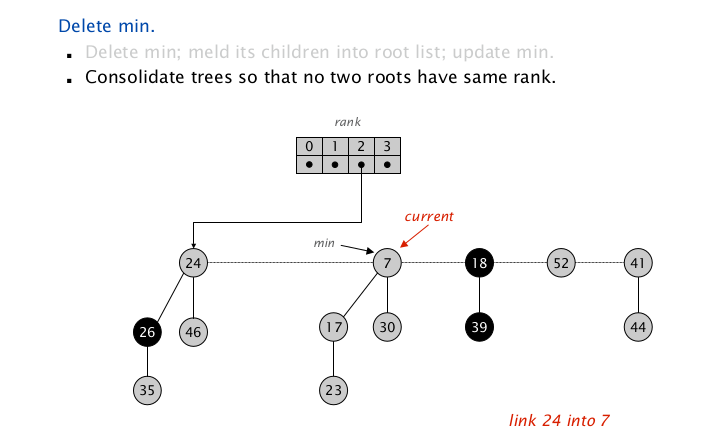
更新后的 $\texttt{node(7)}$ 的 $\texttt{rank += 1} $，为 $2$ ，与 $\texttt{node(24)}$ 相同，继续合并，较大的 $\texttt{rank += 1}$ 插入到 $\texttt{node(7)}$ ；

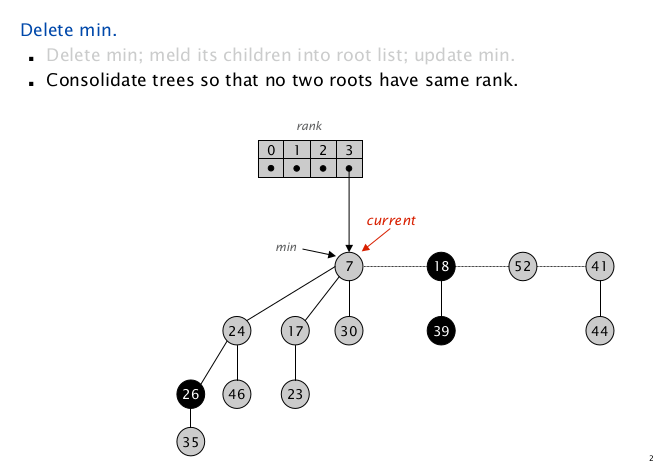
更新后的 $\texttt{node(7)}$ 的 $\texttt{rank += 1} $，为 $3$ ， 没有同 $\texttt{rank}$ 项，把 $\texttt{3 => node(7)}$ 插入到 $\texttt{Map}$ 中，向下扫描；

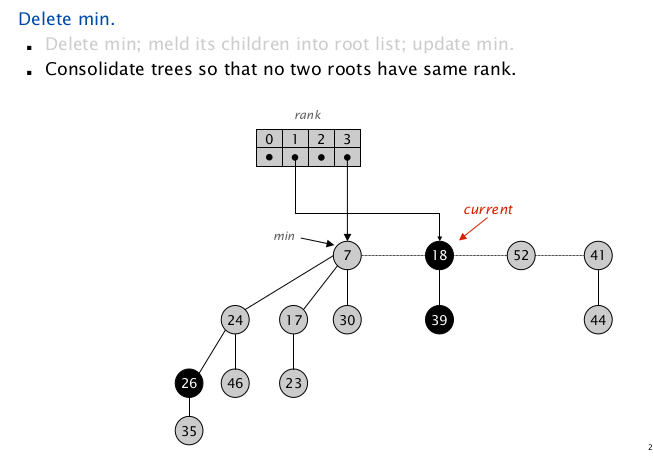
扫描到 $\texttt{node(18)}$ ，$\texttt{rank = 1}$，没有同 $\texttt{rank}$ 项，把 $\texttt{1 => node(18)}$，插入到 $\texttt{Map}$ 中，向下扫描；

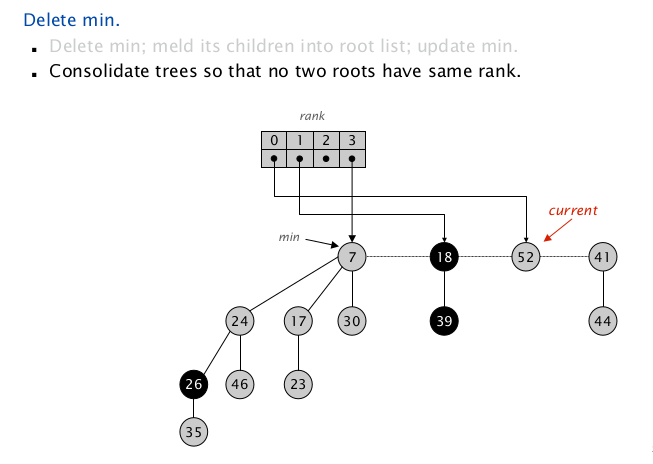
扫描到 $\texttt{node(52)}$ ，$\texttt{rank = 0}$，没有同 $\texttt{rank}$ 项，继续向下；

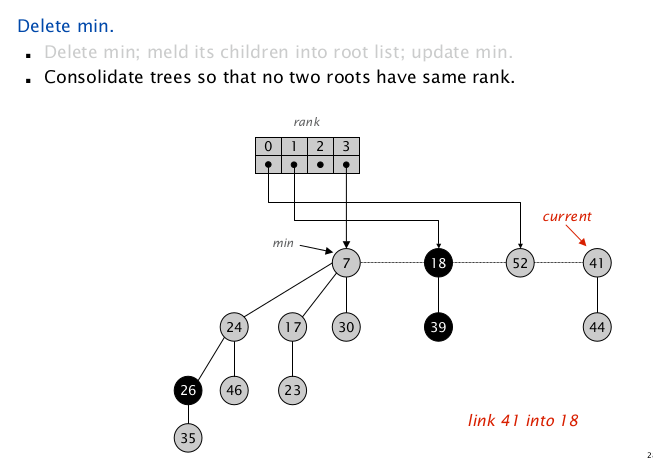
扫描到 $\texttt{node(41)}$ ，$\texttt{rank = 1}$，与 $\texttt{node(18)}$ 的 $\texttt{rank}$ 相同，合并；

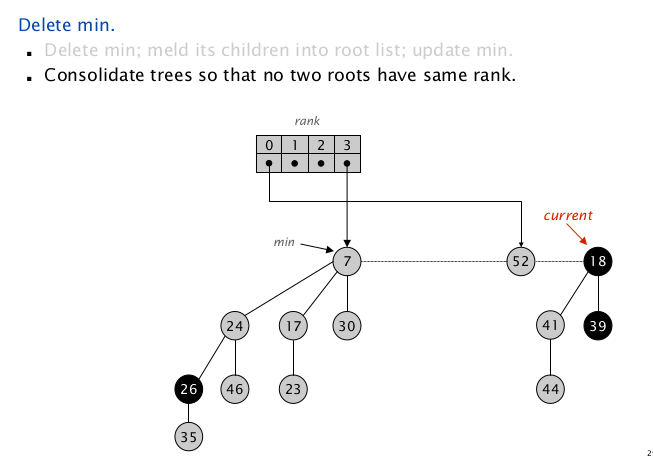
更新后的树 $\texttt{rank = 2}$ ，没有同 $\texttt{rank}$ 项，插入 $\texttt{Map}$ ，向下扫描；

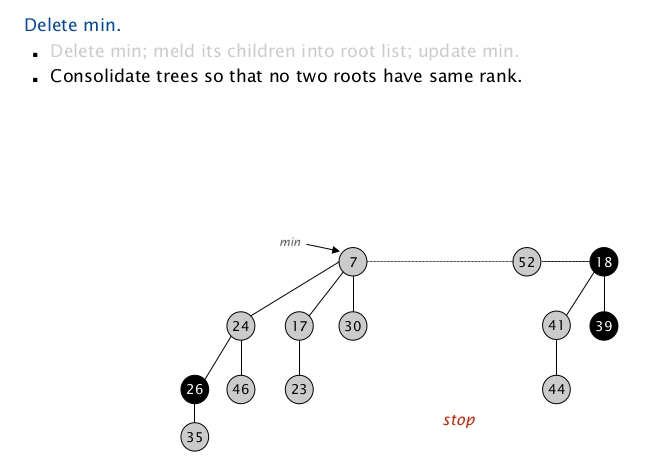
发现所有节点已被扫描完，规整结束。堆的数据结构里维护一个根节点数的变量，用它来指示扫描何时结束 。

复杂度分析

由于每棵树都是二项式树， 扫描最小根孩子节点的实际花费为 $\texttt{rank(H)}$ ，$\texttt{H}$ 为最小根节点的树。扫描根节点链表的实际花费为根节点数，标记为 $\texttt{trees}$ ，所以有实际花费为 $O(\texttt{trees + rank})$ 。

而由于每次规整后的，不存在相同 $\texttt{rank}$ 的树，所以标记 $\texttt{H’}$ 为 $\texttt{rank}$ 最大的树，有 $\texttt{trees} \leqslant \texttt{rank(H’) + 1}$ 。

对于不涉及 decrease-key 操作的F堆来说，每棵树都是严格二项式树，而根据二项式树的性质，标记 $\texttt{H’}$ 的节点数为 $n’$ ， $n’ \lt n$，有 $\texttt{rank(H’)} = \log_2 n’ \lt \log_2 n$ 。

所以摊销时间复杂度为 $O(\log n)$ 。

而对于 decrease-key 操作后的不严格二项式树，由于每棵孩子最多丢失一个孩子，应该仍然保持 $\texttt{rank(H’)}$ ~ ${O(\text{log n})}$ 的性质，后面的性质理论分析部分对此进行了证明，所以摊销时间复杂度仍为 ${O(\text{log n})}$ 。

DecreaseKey 操作

算法

实现 decrease-key ，需要一个额外的编号对节点的索引目录，

同时为了在pop操作时维护这一结构并不破坏时间复杂度，还需要一个反向的节点对编号的目录，进行 O(1) 时间的反查

假设需要更新 $\texttt{key}$ 的节点为 $x$ ，首先检查情况堆的性质是否被破坏：

对于 decrease-key ，堆的性质被破坏的情况就是，节点 $x$ 的 $\texttt{key}$ 比父节点小，对于increase-key，就要检查节点x的子节点的key是否有比其小的 。

如果堆的性质被破坏：

1. 把 $x$ 节点从父节点的孩子中删除，然后推到堆的根的链表上，取消 $x$ 节点的标记（已被规整） ，然后标记父节点（表明它失去过一个孩子节点），姑且把这个操作称为 cut-meld-unmark；

2. 向上递归地执行 cut-meld-unmark ，直到一个未被标记或者是根节点的父节点，然后标记它。

最后检查最小根是否需要被更新。

decrease-key 流程：

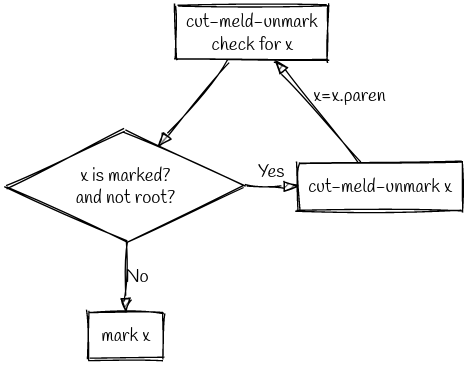
cut-meld-unmark 流程：

图例是一个 decrease-key 的非平凡情况

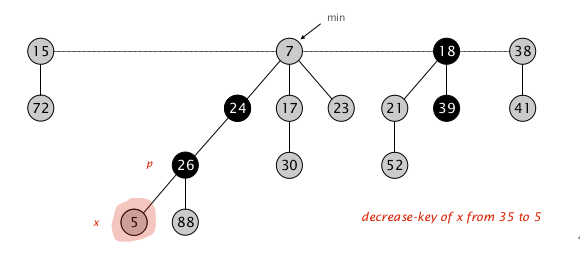
对节点 $x$ 的 $\texttt{key}$ 从 $35$ 降到 $5$

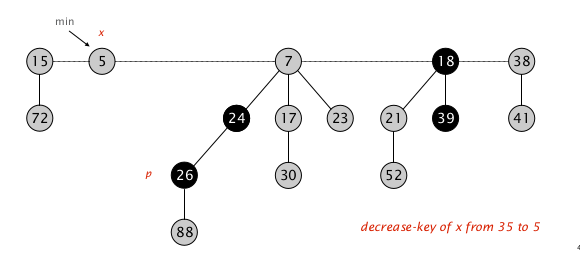
发现堆性质被破坏，先对 $x$ 执行 cut-meld-unmark

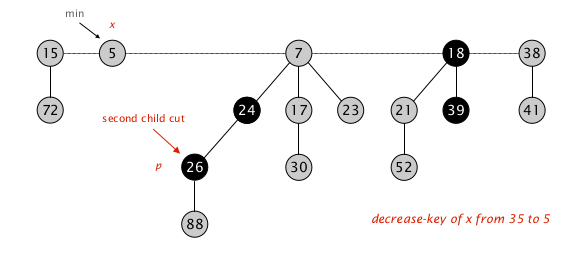
向上递归，发现 $p$ 被标记，意味着 $p$ 之前已经失去过一个孩子，加上这次，已经失去了两个孩子，

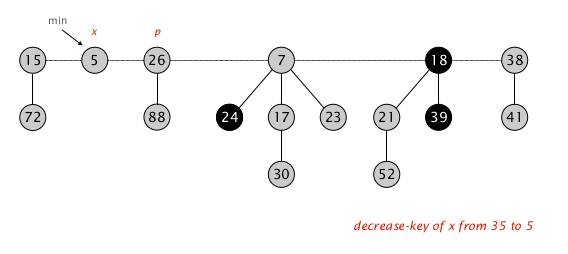
对 $p$ 执行 cut-meld-unmark ，

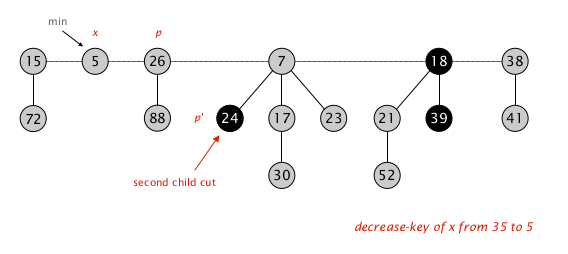
递归地检查 $p$ 的父节点 $p’$ ， $p’$ 也被标记

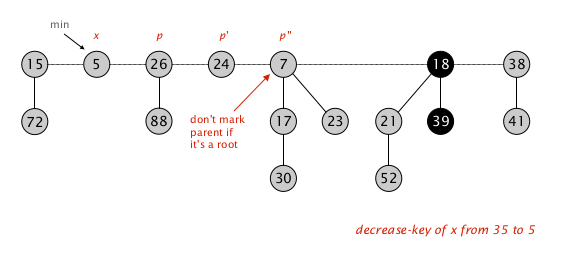
对 $p’$ 执行 cut-meld-unmark ，到了根节点，cut-meld-unmark 整个过程停止，检查最小根，发现 $\texttt{x = 5 < 7}$ ，于是把最小根更新到 $x$ 。

复杂度分析

由于每次操作最多增加一个标记节点，那么平均每次取消的标记节点也是 $1$ ，也就是摊销复杂度是 $O(1)$ 。

其他操作

Union 操作 （Optional）

直接连接两个根链表，不考虑维护索引目录的情况下，那操作就是 $O(1)$ 。

如果需要维护索引目录，索引目录的合并也应该是 $O(1)$ 的时间复杂度。

Remove 操作 （Specific）

1. decrease-key 到 $-\infty$
2. pop

复杂度显然为 $O(\text{log n})$ 。

性质的理论分析

在对斐波那契堆的性质进行分析之前，先要引入几个相关的概念。

黄金比率 （Golden Ratio）

对于两个数 $a$ ，$b$ $a>b>0$ ，有

\[\large\frac{a+b}{a} = \frac{a}{b} = \varphi\]

则称这两个数处于黄金比率，而这个黄金比率 $\varphi$ 可以通过定义

\[\begin{array}{l} & 1 + \frac{b}{a} = \frac{a}{b} = \varphi\\ & 1 + \frac{1}{\large \varphi} = \varphi \end{array}\]

得到它的二次方程 $\varphi + 1 = \varphi^2$

解出两个根，正根 $\varphi = {\large \frac{1+\sqrt{5}}{2}} \approx 1.618$ ，以及负根 $\psi = {\large \frac{1-\sqrt{5}}{2}} \approx -0.618$

斐波那契数 （Fibonacci Number）

\[F_n = \left\{\begin{array}{l} \ 0& &(n = 0) \\ \ 1& &(n = 1) \\ \ F_{n-2} + F_{n-1}& &(n \ge 2) \\ \end{array}\right.\]

$i$	$0$	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$…$
$F_i$	$0$	$1$	$1$	$2$	$3$	$5$	$8$	$13$	$…$

它的封闭表达式

\[F_n = \frac{\varphi^n-\psi^n}{\varphi-\psi} = \frac{\varphi^n-\psi^n}{\sqrt 5}\]

显然它的增长速度也是指数级的。

性质1

基础：

\[\begin{array}{l} &F_2 = 1 = 1 + \sum_{i=0}^{0} F_i\\ &F_3 = 2 = 1 + \sum_{i=0}^{1} F_i \end{array}\]

归纳推理：

\[\begin{array}{l} F_{n+2} &=\ F_n + F_{n+1}\\ &=\ F_n + 1 + \sum_{i=0}^{n-1} F_i\\ &=\ 1 + \sum_{i=0}^{n} F_i \end{array}\]

得到 $F_{n+2} = 1 + \sum_{i=0}^{n} F_i$

性质2

基础：

\[\begin{array}{l} &F_2 =\ 1 \geqslant 1 = \varphi^0\\ &F_3 =\ 2 \geqslant \varphi = \varphi^1 \end{array}\]

归纳推理：

\[\begin{array}{l} F_{n+2} &=\ F_{n+1} + F_{n}\\ &\geqslant \ \varphi^{n-1} + \varphi^{n-2}\\ &=\ \varphi^{n-2}(1 + \varphi)\\ &=\ \varphi^{n-2}\varphi^2\\ &=\ \varphi^n \end{array}\]

得到 $F_{n+2} \geqslant \varphi^n$

斐波那契堆的性质

性质1

对一个 $\texttt{rank}$ 为 $n$ 的节点 $x$ ，按照插入顺序，编号它的孩子 $y_1, y_2, …, y_n$ 。

那么根据二项式树的性质，有 $\texttt{rank(} y_i \texttt{)}= i-1$ 。

考虑到 decrease-key 导致 $y_i$ 最多失去一个孩子

于是有

\[\texttt{rank}({\large y_i}) \geqslant \ \left \{\begin{array}{l} \ 0 &(i=1)\\ \ i - 2 &(i \geqslant 2)\\ \end{array}\right.\]

性质2

假设 $\texttt{size(k)}$ ，为 $\texttt{rank}$ 为 $k$ 的节点的可能的最小结点数

基础：

\[\begin{array}{l} &\texttt{size}(0) =\ 1 = F_2 \geqslant F_2 \\ &\texttt{size}(1) =\ 2 = F_3 \geqslant F_3 \\ \end{array}\]

归纳推理：

\[\begin{array}{l} size(k) &\geqslant 1 + \sum_{i=1}^{k} \texttt{size(rank(}y_i\texttt{))}\\ &= 1 + \texttt{size(rank(}y_1\texttt{))} + \sum_{i=2}^{k} \texttt{size(rank(}y_i\texttt{))}\\ &\geqslant 1 + \texttt{size(0)} + \sum_{i=2}^{k} \texttt{size(rank(i-2))}\\ &\geqslant 1 + 1 + \sum_{i=2}^{k} \texttt{size(} F_i \texttt{)}\\ &= 1 + \sum_{i=0}^{k} \texttt{size(} F_i\texttt{)}\\ &= F_{k+2}\\ &\geqslant \varphi^{k} \end{array}\]

于是有

\[\texttt{size(k)} \geqslant F_{k+2} \geqslant \varphi^{k}\ \ \ (k \geqslant 0)\]

根据这个性质，两边取 $log$ ，得到 $\log_{\varphi}^\texttt{size(k)} \geqslant k = rank$ 。

回顾前面 pop 的时间复杂度分析，$\texttt{rank}$ ~ $O(log_{\varphi}^{\texttt{size(k)}})$ ~ $O(\log n)$，也就是说我们在理论上证明了 decrease-key 导致的不严格二项式树，仍然不影响它的 $O(\text{log n})$ 的时间复杂度。

后续：具体实现（Rust）

引用