树状数组

Algorithm

April 24, 2023

本文主要参考 OI-wiki 以及 cp-algorithms.com 相关页面¹

树状数组（Binary Indexed Tree, Fenwick Tree）²，以下简称 BIT，其命名是由于 Peter Fenwick 在 1994 年发表的文章里描述了这一结构，它的本质是通过高效地计算数组的前缀和来解决相关的问题。

VS 分段树

因此树状数组也能解决诸如给定区间的和之类的问题，只要这类问题可以转换为几个前缀和的运算。

而前面介绍过的分段树也可以解决这类问题，区别是：

时间复杂度：

都是 $O(\text{log}n)$，但树状数组的性能远好于分段树，测算可能差了 10 倍

空间复杂度：

都是 $O(n)$ ，但树状数组空间和源数组大小相等，是 $1n$ ，而分段树 DFS 型需要 $2n$ ，BFS 型更是需要 $4n$

代码复杂度

树状数组的代码更简单

因此只要能用树状数组解决的问题，都优先使用树状数组³。

VS 前缀和

如果不做区间的更新，那么树状数组比普通地前缀和没有任何优势，毕竟单次查询还要 $O(n\text{log}n)$

概念

可以通过一个图直接看一下树状数组的结构⁴，下图是数组 $a[1..16]$ 的 BIT 结构：

图中每个节点都代表一段长度至少为 $1$ 的区间，比如 $2$ 包含区间 $[1..2]$ ，$4$ 包含区间 $[1..4]$ ，$6$ 包含区间 $[5..6]$ 。

让我们省略掉重复的元素，会对结构看得更清晰：

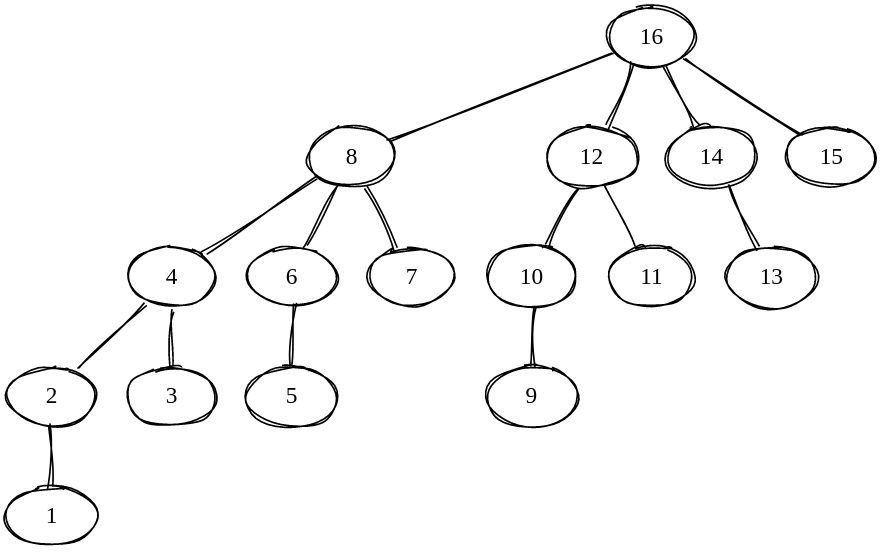
我们发现 BIT 实际上就是由我们前面介绍斐波那契堆时提过的二项树组成。

比如 $8$ 是一棵 $\text{rank}=3$ 的二项树，$12$ 是一棵 $\text{rank}=2$ 的二项树。

二项堆是说每个孩子都是 $\text{rank}$ 独特的二项树，同时满足小顶堆的性质，而 BIT 自然不需要满足堆的性质，但是也要求 $\text{rank}$ 独特，并且 rank 是连续的并且严格递减的，比如上述 BIT 分别是由 $\text{rank}= 3，2，1，0$ 的二项树组成。

树状数组就是在每个位置存储所代表的区间的元素的和。

分片长度

那么如何计算某个索引位置代表的区间的长度呢？

观察发现，一个序号越是能被更大的 $2$ 的幂整除，代表的区间就越大。

实际上，区间长度，或者说区间的元素数，就是由序号的二进制的最低有效位⁵与后面 $0$ 构成的数字决定的。

比如 $12 = (1100)_2$ ，最低有效位是 $3$ ，与后面的 $0$ 构成的数字是 $(100)_2=4$ ，代表 4 ；

比如 $15 = (1111)_2$ ，最低有效位是 $1$ ，与后面的 $0$ 构成的数字是 $(1)_2=1$ ，代表 1

那么如何求取一个序号的最低有效位构成的数字呢？

假设序号为 x，那么对 x 按位取反再加 1 ，再按位与原值，就可以求出 x 的最低有效位的构成数字。

为什么是这样呢？

仔细考虑一下这个过程就清楚了：

根据定义，最低有效位是 $1$ ，后面更低位全都是 $0$ ，比如 $(100)_2$ ，$x$ 取反后，变为 $(011)_2$ ，加一后，又变回 $(100)_2$ ，因此按位与时最低有效位的 $1$ 以及后面的更低位的 $0$ 被原封不动地保留下来；
由于进位已经停在最低有效位上，因此更高的位只是取反，按位与后就被清除掉了

这样就得到了最低有效位和后面的 $0$ 构成的数字。

于是我们证明了 x & (!x+1) 可以得到区间的长度。

但是这个书写形式还可以简化

因为整型数字在计算机中的存储形式是 2 的补码（two’s complement），按照定义，对于一个数取反加一就得到了它对应的负值。

因此区间长度可以简化为 x & -x 。

实现

定义下结构，这里继续使用了前面分段树里定义的抽象组件：

#[repr(transparent)]
pub struct BIT<T> {
    data: Vec<T>,
}

建树

首先我们可以进一步通过观察上述的图，发现两个 BIT 的性质：

每个位置，都可以由它自身和它的直接孩子求和得到，比如 $t[4] = a[4] + t[3] + t[2]$ ；
每个位置，它到直接父母的距离就是它所代表的区间的大小，或者说它代表了父节点所辖地一半的元素数，比如 $4$ 到直接父母 $8$ 的距离就是 $4$ 所代表区间 $[1..4]$ 的长度，也就是 $4$

利用上述性质，可以直接在 $O(n)$ 的时间复杂度内完成的树的构造：

用 $0$ 初始化 BIT，遍历原数组 $a[..]$ ，把它的每个值加到 BIT 对应位置，然后再用 BIT 这个位置的数值每次更新它的直接父母。

macro_rules! range_len {
    ($i:ident) => {
        (($i as isize + 1) & -($i as isize + 1)) as usize
    };
}

impl<T> BIT<T> {
    pub fn len(&self) -> usize {
        self.data.len()
    }
}

impl<T> BIT<T>
where
    T: Sum + Clone + Add<Output = T> + AddAssign,
{
    pub fn new<U>(raw: &[U]) -> Self
    where
        U: Clone + Into<T>,
    {
        assert!(!raw.is_empty());

        let data = Self::build(raw);

        Self { data }
    }

    fn build<U>(raw: &[U]) -> Vec<T>
    where
        U: Clone + Into<T>,
    {
        let mut data: Vec<T> = vec![zero!(); raw.len()];

        for i in 0..raw.len() {
            data[i] += raw[i].clone().into();

            // direct parent
            let j = i + range_len!(i);

            if j < raw.len() {
                let data_i = data[i].clone();

                data[j] += data_i;
            }
        }

        data
    }
}

计算区间长度的时候，如果是基于 $0$ 的数组，注意需要把索引位置加一，得到前面讨论的代表数量的编号。

前缀和

计算前缀和也只需统计查询位置前面的区间，方法是每次向前跳索引代表的一个区间的长度：

impl<T> BIT<T>
where
    T: Sum + Clone + Add<Output = T> + AddAssign,
{
    pub fn prefix(&self, mut i: usize) -> T {
        i = std::cmp::min(i, self.data.len() - 1);

        let mut acc = zero!();

        loop {
            acc += self.data[i].clone();

            if i < range_len!(i) {
                break;
            }

            i -= range_len!(i);
        }

        acc
    }
}

计算两个端点的前缀和，就可以求出给定区间的区间和：

impl<T> BIT<T>
where
    T: Sum + Clone + Add<Output = T> + AddAssign,
{
    pub fn query<R: RangeBounds<usize>>(&self, range: R) -> T
    where
        T: Sub<T, Output = T>,
    {
        let Range { start, end } = std::slice::range(range, ..self.len());

        let (l, r) = (start, end - 1);

        self.prefix(r) - if l > 0 { self.prefix(l - 1) } else { zero!() }
    }
}

宏 parse_range 来源于前面分段树里面定义的宏，给出 $[l, r]$ 的两个端点 $l$ 和 $r$ 。

批量更新

除了查询区间和之类的问题，树状数组也可以处理对原数组的批量更新的问题。

单点查询

最简单的情况是批量更新后，只要求对某一个点进行查询。

这时，用一个 BIT 保存每个位置更新的累加值，初始化为 0 。

当查询原数组某个点的值时，就是求取 BIT 上该点的前缀和，再加上原值。

那么如何更新 BIT 的累加值？

当对给定区间 $[l, r]$ 累加 $x$ 时，就在 $l$ 点处增加 $x$ ，并在 $r+1$ 点处减少 $x$ ，来取消对后面点的前缀和的影响。

impl BIT<i32> {
    pub fn range_add_for_origin<R: RangeBounds<usize>>(
        &mut self,
        range: R,
        addend: i32,
    ) {
        let Range { start, end } = std::slice::range(range, ..self.len());
        let (l, r) = (start, end - 1);

        self.add(l, addend);
        self.add(r + 1, -addend);
    }
}

对 BIT 某点上进行更新的时候，需要连带更新它的所有父节点

impl<T> BIT<T>
where
    T: Sum + Clone + Add<Output = T> + AddAssign,
{          
    pub fn add(&mut self, mut i: usize, addend: T) {
        while i < self.data.len() {
            self.data[i] += addend.clone();

            i += range_len!(i);
        }
    }
}

区间和查询

如果批量更新后还要查询区间和（的更新），那么前面（通过前缀和的方式）仅对某一个点的更新值的记录就不够了。

怎么做呢？

解决方法并不那么直观，不妨先一步一步地考虑：

如果给定区间 $[l, r]$ 上批量加上 $x$ ，那么加值的前缀和应该是这样的：

\[\text{sum}[0,i]= \begin{cases} 0 & i < l \\\\ x \cdot (i-l+1) & l \leqslant i \leqslant r \\\\ x \cdot (r-l+1) & r \lt i \\ \end{cases}\]

这个前缀和可以拆分为两部分：

\[\text{sum}[0,i]= \begin{cases} 0 \cdot i - 0 & i < l \\\\ x\cdot i - x\cdot (l-1) & l \leqslant i \leqslant r \\\\ (x-x)\cdot i - (x \cdot (l-1) - x\cdot r) & r \lt i \\ \end{cases}\]

可以用前面区间更新后单点查询的思路，用一个树状数组 $\text{B}_1$ 表示前一部分的数值：

\[\text{sum}(\text{B}_1)[0,i]= \begin{cases} 0& i < l \\\\ x & l \leqslant i \leqslant r \\\\ x-x & r \lt i \\ \end{cases}\]

用另一个树状数组 $\text{B}_2$ ，表示后一部分的值：

\[\text{sum}(\text{B}_2)[0,i]= \begin{cases} 0 & i < l \\\\ x\cdot (l-1) & l \leqslant i \leqslant r \\\\ x \cdot (l-1) - x\cdot r & r \lt i \\ \end{cases}\]

计算 $\text{B}_1$：

\[\begin{array}{l} \text{add}(\text{B}_1,\ l,\ x)\\ \text{add}(\text{B}_1,\ r+1,\ -x) \end{array}\]

计算 $\text{B}_2$：

\[\begin{array}{l} \text{add}(\text{B}_2,\ l,\ x\cdot(l-1))\\ \text{add}(\text{B}_2,\ r+1,\ -x\cdot r) \end{array}\]

前缀和：

\[\text{sum}[0,i] = \text{sum}(\text{B}_1)\cdot i - \text{sum}(\text{B}_2)\]

给定区间 $[l, r]$ 的累积更新的和：

\[\text{sum}[l, r] = \text{sum}[0,r] - \text{sum}[0,l-1]\]

再加上原数组的区间和，就是更新后的数组的区间和。

实现

#[repr(transparent)]
pub struct RangeAddQuerySum<T>(BIT<T>);

impl BIT<i32> {
    pub fn create_range_add_query_sum_aux(&self)
    -> RangeAddQuerySum<i32>
    {
        RangeAddQuerySum::new(self.len())
    }
}

impl RangeAddQuerySum<i32> {
    pub fn new(cap: usize) -> Self {
        Self(BIT { data: vec![0; cap] })
    }

    pub fn add<R: RangeBounds<usize>>(&mut self, range: R, addend: i32) {
        let Range { start, end } = std::slice::range(range, ..self.0.len());

        let (l, r) = (start, end - 1);
        self.0.add(l, addend * (l as i32 - 1));
        self.0.add(r + 1, -addend * r as i32);
    }

    /// Get update accumulation
    pub fn query<R: RangeBounds<usize>>(
        &self,
        range: R,
        bit1: &BIT<i32>,
    ) -> i32 {
        let Range { start, end } = std::slice::range(range, ..self.0.len());

        let (l, r) = (start, end - 1);
        self.prefix(r, bit1) - if l > 0 { self.prefix(l - 1, bit1) } else { 0 }
    }

    fn prefix(&self, i: usize, bit1: &BIT<i32>) -> i32 {
        bit1.prefix(i) * i as i32 - self.0.prefix(i)
    }
}

这种实现可以利用之前为批量更新单点查询建立的树状数组。

注解

没有找到讲得特别清楚又特别详细的资料，cp-algorithms.com 本篇的从风格到质量都有失水准，反而 OI-wiki 还比较详细，明明是早已有的概念，却有相当多的内容上是近期更新的 ↩
我喜欢这个命名，简单形象不故弄玄虚 ↩
但是分段树能通过拆分区间，处理很多树状数组处理不了的在连续区间上的查询问题 ↩
图片来源于 https://www.baeldung.com/cs/fenwick-tree ↩
数字的二进制表示里最低的一个 $1$ 的位置 ↩