质数筛子
质数筛子的原理是质因数分解。
前言
有几个关于质数筛子的总结性观察：
观察 1
不使用分段技术的（可用的）质数筛子，不管它的时间复杂度和空间复杂度在理论上是超线性、线性还是亚线性，在实践上都可以视为线性。
这是因为，
- 它们的区别往往只在于 $ N\log\log N$, $N$ 和 $\large\frac{N}{\log\log N}$ ，而 $\log\log N$ 对于一个 64 位机的指针宽度的最大数字也就是 $\log\log64 = 8$ ，很可能还不如一个常数大；
- 在实现上，超线性和线性算法有数据结构简单的优势，而亚线性算法则有规定时间复杂度内实际实现不了或者常数很大的劣势。
观察 2
质数筛子的时间复杂度和空间复杂度不可能同时为亚线性。
观察 3
能否应用分段技术是筛子算法先进与否的分水岭。
能运用分段技术，实质就是可以进行独立任务分解，这样一方面可以将空间占用降为 $O(\sqrt N)$ ，而通常算法的瓶颈在于空间占用；另一方面也可以在多核架构下进行并行化处理。
以下介绍的筛子按照发明的时间顺序进行排列， 标题括号里的是对其总体评价。
Eratosthenes 筛子（√√√）
Eratosthenes 筛子，简称作E-筛子，属于是非常古老、简单的一种筛子算法：
- 在对整个范围一遍扫描的过程中，开始先逐个数检查质性；
- 当发现一个质数 $p$ 时，就把它的乘积： $2p, 3p, \dots , \lfloor n/p\rfloor p$ ，都标记为合数；
- 这样在继续扫描的过程中发现被标记为合数的就直接跳过，直到发现下一个质数，然后重复步骤2直到 $n$
实际上我们标记合数的方法是追踪所有小于它的质数，因为根据之前所讲的正整数唯一分解定理，也就是所有的合数都可以做质因数分解，一定存在一个严格比它小的质数可以除它。这样的话，如果我们是从第一个质数开始，那么实际上：
- 标记合数的过程不需要从 $2p$ 开始，而是直接从 $p\cdot p$ 开始，因为所有 $\lt p$ 的合数已经被更小的质数标记过了；
- 最外轮的扫描只到 $\lfloor \sqrt{n} \rfloor$ 即可，因为作为合数的因子对，只需要通过那些较小的就可以完成合数的标记了
样例代码
use bit_vec::BitVec;
macro_rules! sieve_spec_case {
($n: ident; [0, 1]) => { {
let n = $n;
if n < 2 {
return Box::new(std::iter::empty());
}
} };
($n: ident; [0, 2]) => { {
let n = $n;
sieve_spec_case!(n; [0, 1]);
if n == 2 {
return Box::new(std::iter::once(2));
}
} };
($n: ident; [0, 4]) => { {
let n = $n;
sieve_spec_case!($n; [0, 2]);
if n <= 4 {
return Box::new([2, 3].into_iter());
}
} };
}
pub fn e_sieve(n: usize) -> Box<dyn Iterator<Item = usize>> {
sieve_spec_case!(n; [0, 2]);
let mut bits = BitVec::from_elem(n + 1, true);
for i in 2..=n.isqrt() {
if bits[i] {
for j in (i * i..=n).step_by(i) {
bits.set(j, false);
}
}
}
Box::new(
bits.into_iter()
.enumerate()
.skip(2)
.filter_map(|(i, flag)| if flag { Some(i) } else { None }),
)
}
复杂度分析
每查找到一个质数 $p$ ，就需要 $N/p$ 的操作次数，因此总的操作数为 $\displaystyle \sum_{ p\leqslant \sqrt{N}} N/p $ 。而根据已知的结论，来自1 chapter 22 的：$\displaystyle \sum_{p \leqslant x} \frac{1}{p} = \log\log x + O(1)$ ，可以得到算法的最坏时间复杂度为 $O(N\log\log N)$ 。
算法评价
是次快的算法，而且非常简单，虽然空间占用 $O(N)$，但常数非常小（等效 $O(\large\frac{N}{\log\log N})$ 说是）。
分段 Eratosthenes 筛（√√√）
分段处理可以把空间占用从 $O(N)$ 降到 $O(\sqrt{N})$ ，指数级地缓解算法的空间占用。
方法是可以预计算出所有到 $\sqrt{N}$ 为止的质数，根据前面已知，所有 $\leqslant N$ 范围内的合数都可以由预计算出的质数构造出，只需要知到这些质数的乘积落在每个分段上的第一个数，就可以标记完所有这个分段的合数。
而如何知道质数 $p$ （的乘积）落在某个分段区间的第一个数呢？只需要知道分段的左边缘 $l$ ，那么易知落点为 $l+p-(l\mod{p})$ 。
样例代码
/// Space: O(\sqrt{n})
pub fn e_seg_sieve(n: usize) -> Box<dyn Iterator<Item = usize>> {
sieve_spec_case!(n; [0, 4]);
let delta = n.isqrt();
let pris = e_sieve(delta).collect::<Vec<usize>>();
let mut acc = vec![];
let mut l = delta;
while l < n {
acc.extend(e_seg_sieve_0(&pris, l, min(delta, n - l)));
l += delta;
}
Box::new(pris.into_iter().chain(acc.into_iter()))
}
/// 0. p^2 >= l+delta
/// 1. pris from 0..x, no empty.
/// 2. return (l, l+delta]
fn e_seg_sieve_0<'a>(
pris: &'a [usize],
l: usize,
delta: usize,
) -> impl Iterator<Item = usize> + 'a {
debug_assert!(!pris.is_empty());
std::iter::from_coroutine(
#[coroutine]
move || {
let mut seg = BitVec::from_elem(delta + 1, true);
for &p in pris.iter() {
for i in (p - l % p..=delta).step_by(p) {
seg.set(i, false);
}
}
for (i, flag) in seg.into_iter().enumerate().skip(1) {
if flag {
yield l + i
}
}
},
)
}
复杂度分析
这样主要辅助空间是两个 $\sqrt{N}$ bit 的数组，因此空间复杂度为 $O(\sqrt{N})$ 。而当分段大小为 $\sqrt{N}$ 时，总的时间复杂度仍然是 $O(N\log\log N)$ 。
算法评价
速度排名属于第三档，但仍然简单而且足够快，重要的是使用了分片技术！
Sundaram 筛子（√√√）
Sundaram 筛子2 ，是基于奇数因子分解 $2k+1$ 的筛子。
方法是检查所有 $i + j + 2ij\quad (1\leqslant i \leqslant j)$ 形式的数字，筛掉所有奇数里的合数。
原理如下：
\[\begin{array}{ll} 2k+1&= 2\cdot(i+j+2ij) + 1 \\ &= 2i + 2j + 4ij + 1 \\ &= (2i+1)(2j+1) \end{array}\]也就是说所有由 $k=i + j + 2ij$ 构成的奇数都是合数；反过来，一个奇数合数也只能是分解为两个奇数之积。
样例代码
pub fn sundaram_sieve(n: usize) -> Box<dyn Iterator<Item = usize>> {
sieve_spec_case!(n; [0, 3]);
let k = (n - 1) / 2;
let mut bits = BitVec::from_elem(k + 1, true);
for i in 1..=k {
for j in i..=k {
if i + j + 2 * i * j > k {
break;
}
bits.set(i + j + 2 * i * j, false);
}
}
Box::new(
once(2).chain(bits.into_iter().enumerate().skip(1).filter_map(
|(i, flag)| if flag { Some(2 * i + 1) } else { None },
)),
)
}
算法改进
但是与其去构造奇数，不如直接检测所有奇数，这样还避免了很多 $i + j + 2ij \gt k$ 时的空转。
pub fn sundaram_sieve_improved(n: usize) -> Box<dyn Iterator<Item = usize>> {
sieve_spec_case!(n; [0, 3]);
let k: usize = (n - 1) / 2;
let mut bits = BitVec::from_elem(k + 1, true);
for odd1 in (3..=n.isqrt()).step_by(2) {
// for c in (odd1 * odd1..=n).step_by(2 * odd1) {
// bits.set((c - 1) / 2, false);
// }
for odd2 in (odd1..).step_by(2) {
if odd1 * odd2 > n {
break;
}
bits.set((odd1 * odd2 - 1) / 2, false);
}
}
Box::new(
once(2).chain(bits.into_iter().enumerate().skip(1).filter_map(
|(i, flag)| if flag { Some(2 * i + 1) } else { None },
)),
)
}
这里注解了一段乘法改加法的代码，在一些经典算法论文，通常是上世纪九十年代以前的那些，很喜欢搞乘法变加法的优化，但现在应该被视为过早优化，因为乘法很容易，也很普遍地在更低层次的软件和硬件上做优化，在应用端算法上做加法替代实现反而构成了一种明显的反优化。3
另一方面，除法倒是还有算法上优化的必要。
复杂度分析
时间复杂度 $O(N\log\log N)$ ，空间复杂度 $O(N)$ 。
算法评价
实践时间性能非常好，是最快的一档，特别是改进的版本，甚至比 SFWS 还要快一点点。
Mairson 筛子（√）
仔细考虑下，前面E-筛子的计算过程还有重复的操作，就是有一些合数比如 $C = p_m^i\cdot p_n^j\cdot p_q^k,\ (p_m\neq p_n\neq p_q)$ 它会被不同的质数 $p_m, p_n, p_q$ 重复标记，这也是它超线性时间复杂的原因。
Mairson 筛子4的实质是取消这些重复标记的过程，把问题转化为线性，为此每用一个质数 $p$ 标记完一些合数后，就要把这些合数排除在后续的标记范围里。
道理都懂，问题是怎么排除，Mairson 很实在地给出了具体的数据结构，也是大家根据这个具体情况自然而然能想到的，即，一个基于数组的双向链表：
- 一般情况下，既然是集合的操作，那么就可以考虑哈希集合，但从冗余度上讲空间占用会是所需的几倍；而质数的情况是值空间有限，实际上都是连续的自然数，完全可以放进一个数组里，用数组的下标作为索引的键；
- 再考虑到从集合删除元素的操作需要是常数级 $O(1)$ ，那么就需要是一个链表，而且是双向链表；
- 数组每个位置存储下一个节点的索引坐标，这样在标记某个数被删除时，只需要修改它的左右节点，就可以跳过这个节点；
- 这个链表的头可以就是数组头，而它的尾部只需要靠存储值为零进行标记，同时这种设计使得这个链表在首尾连成了一个环，头部也形成了一个自环，体现了一种优雅。
于是我们构造这个结构如下：
// n > 0
let mut forward: Vec<usize> = (1..=n).chain(once(0)).collect();
let mut backward: Vec<usize> = once(0).chain(0..=n - 1).collect();
用 forward 数组记录前向链接、backward 数组记录后向链接，开始时它们应该初始化为：
这样当从集合里删除某个数 $i$ 时，只需要：
forward[backward[i]] = forward[i];
backward[forward[i]] = backward[i];
这样整个算法过程的其他部分和之前的 E-筛子一样。
样例代码
pub fn mairson_sieve(n: usize) -> impl Iterator<Item = usize> {
std::iter::from_coroutine(
#[coroutine]
move || {
if n == 0 {
return;
}
let mut forward: Vec<usize> = (1..=n).chain(once(0)).collect();
let mut backward: Vec<usize> = once(0).chain(0..=n - 1).collect();
// lpf (least prime factor)
let mut p = 2usize;
while p * p <= n {
/* collected andthen remove all number which lpf is p from S. */
let mut c = vec![];
let mut f = p;
while p * f <= n {
// remove p*f from S
c.push(p * f);
f = forward[f];
}
for i in c {
forward[backward[i]] = forward[i];
backward[forward[i]] = backward[i];
}
p = forward[p];
}
let mut i = 1;
while forward[i] != 0 {
yield forward[i];
i = forward[i];
}
},
)
}
需要注意得是，不能标记一个合数 $f$ 就立刻把它删除，因为还需要依靠它去标记 $p\cdot f$ 以及其它后续的合数。所以必须要先收集一个质数 $p$ 标记的所有合数，然后再把它们删除。
算法改进
如果可以从由 $p$ 组成的最大的那个合数开始逆序标记，那么就可以立刻删除 $p\cdot f$ 而不需要先收集起来。5
这可以带来一些性能的提升和空间的节省。
那么问题就变成如何找到最大待标记数对应的 $f$ ，或者如何追踪它。
我们一步步地考虑这个问题，开始时 $p_1 = 2$ ，那么 $f_{\text{max}} = \large\lfloor \frac{n}{2} \rfloor$ ，在用 $p_1$ 标记完一轮后，再从 $f_{\text{max}}$ 开始逐个向下检查，直到找到一个还在链表上的数，然后从它开始沿着链表倒序查找，找到一个满足 $p_2 \cdot f \leqslant n$ 的值作为第二轮 $p_2$ 对应的 $f_{\text{max}}$ 。
这样的话在从链表上删除某个数的时候，还需要在对应下标的某个数组上额外标记它，以便于能在 $O(1)$ 的时间里检查某个数是否在链表上。backward 还需要用来向前查找，可以用 forward[i] = n+1 ，表示 $i$ 被删除。
这样的话标记结束的条件也可以用 $f_{\text{max}} \geqslant p$ 来代替。
//...
let mut f_max = n / 2;
while f_max >= p {
let mut f = f_max;
while f >= p {
forward[backward[p*f]] = forward[p*f];
backward[forward[p*f]] = backward[p*f];
forward[p*f] = n+1; // flag it
f = backward[f];
}
p = forward[p];
if forward[f_max] == n+1 { f_max -= 1; }
while f_max * p > n { f_max = backward[f_max]; }
}
//...
有一个观察，但是还无法证明，链表上相邻的两个数不会被同一个 $p$ 标记6，那么下一轮的 f_max = backward[f_max] 。
这样改进后的完整算法如下：
pub fn mairson_sieve(n: usize) -> impl Iterator<Item = usize> {
std::iter::from_coroutine(
#[coroutine]
move || {
if n == 0 {
return;
}
let mut forward: Vec<usize> = (1..=n).chain(once(0)).collect();
let mut backward: Vec<usize> = once(0).chain(0..=n - 1).collect();
// lpf (least prime factor)
let mut p = 2usize;
let mut f_max = n / 2;
while f_max >= p {
let mut f = f_max;
while f >= p {
forward[backward[p*f]] = forward[p*f];
backward[forward[p*f]] = backward[p*f];
forward[p*f] = n+1; // flag it
f = backward[f];
}
p = forward[p];
if forward[f_max] == n+1 { f_max = backward[f_max]; }
while f_max * p > n { f_max = backward[f_max]; }
}
let mut i = 1;
while forward[i] != 0 {
yield forward[i];
i = forward[i];
}
},
)
}
复杂度分析
显然，时间复杂度和空间复杂度均为 $O(N)$ 。
算法评价
一般，跑得不快，内存占用在线性算法里也属于常数比较大的。
轮子与轮筛（-）
定义轮子
轮子（wheel）是由头几个质数的乘积构成的一个空间，空间里的数都与这些质数互质。
这头几个质数的乘积叫做质数阶乘，记作 $p_k\sharp = \displaystyle\prod_{i=1}^{k}{p_i} = p_1\times p_2 \ \times ..\ p_k$ 9，在前面质数基础的质性测试一节已经接触过这个概念，于是有轮子 $W_k$（第 $k$ 个轮子）：
\[W_k = \lbrace x\vert\ x \bot p_k\sharp,\ (1\leqslant x \leqslant p_k\sharp) \rbrace\]和 $W_k$ 的模 $p_k\sharp$ 的同余数集 $W_k^*$ ：
\[W_k^* = \lbrace x\vert\ x \pmod {p_k\sharp} \in W_k \rbrace\]显然，任何一个 $x \in W_k^*$ 都和 $p_1,\ p_2\ ..,\ p_k$ 互质，这可以用来把很多非质数提前筛出去，并且如果 $x \lt p_{k+1}^2$ ，那么 $x$ 一定是个质数。
自然可以想到，如果能构造一个更大的轮子，那么显然可以更有效地筛选质数，可以在更大范围内直接确保 $x$ 就是个质数。
构造轮子
首先，我们知道 $W_1 = \lbrace 1 \rbrace$；
其次，Pritchard 给出了一个非常形象的示意图来演示如何通过“滚动”和删除一些点，从 $W_k$ 构造出 $W_{k+1}$8
图-轮子
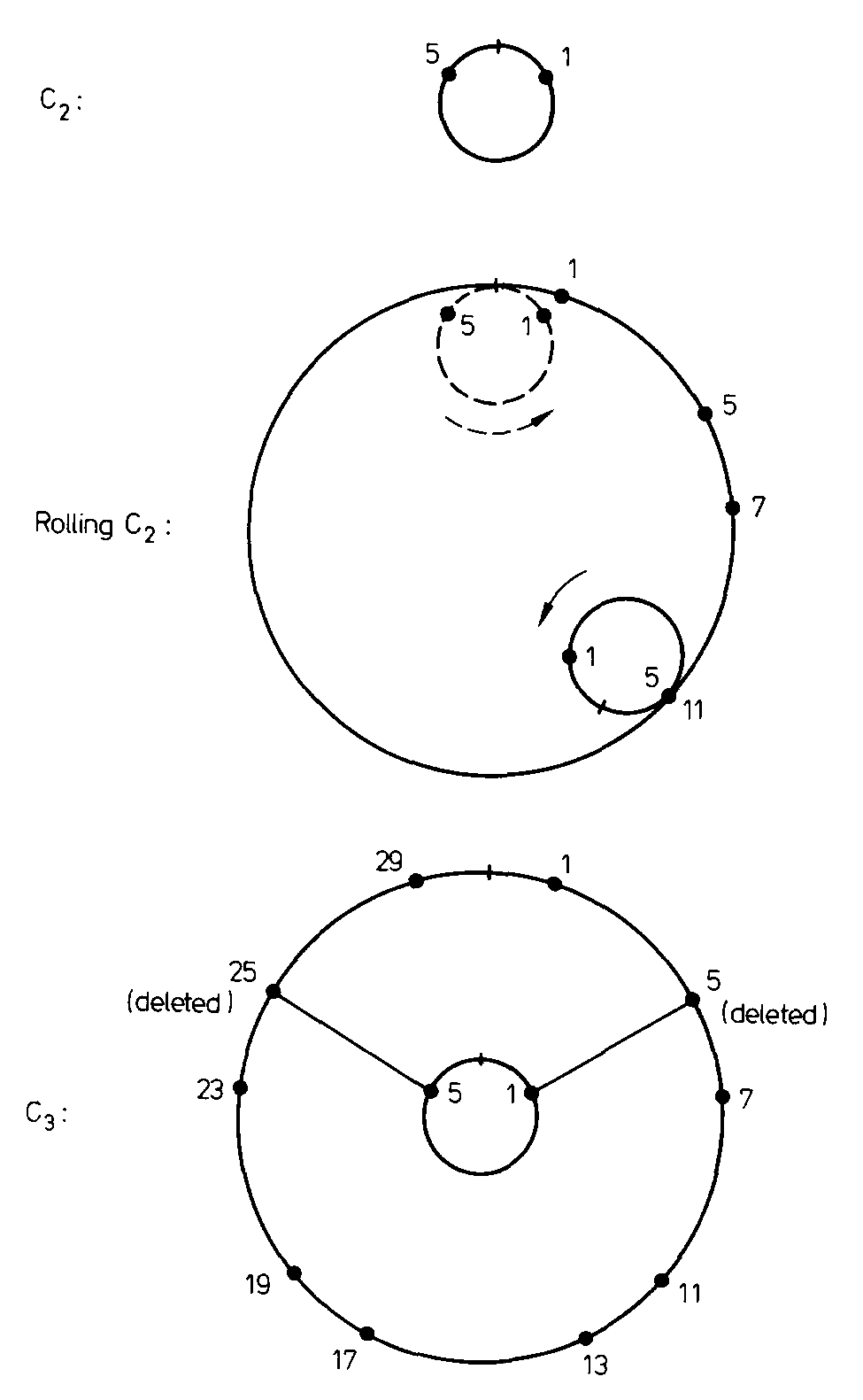
直接看图有些不明所以，让我们慢慢解释。
可以定义周长为 $p_k \sharp$ 的圆圈 $C_k$，$x \in W_k$ 则是它上面沿顺时针标记的点。
从 $W_k$ 构造出 $W_{k+1}$：
-
$W_k$ “滚动” $p_{k+1}$ 圈就可以得到下一个轮子 $W_{k+1}$ 轮廓；
-
再根据 $W_{k+1}$ 定义，删除满足 $x’ = p_{k+1}\cdot x,\ (x\in W_k)$ 的“同辐条点”，因为 $x’ \vert p_{k+1}$
轮子性质
性质 1
如上图所示，通过 $C_k$ 滚动构建 $C_{k+1}$ 后根据 $W_{k+1}$ 定义需要删除的点 $x’$，与原先 $C_k$ 上的点在同一根辐条上，或者说它们弧度相同。
因为 $x’ = p_{k+1}\cdot x$ 。
性质 1.1
这样我们知道 $\vert W_{k+1}\vert = (p_{k+1}-1)\cdot \vert W_k \vert$。
而我们知道 $\vert W_1\vert = 1$ ，通过递推，可以得到 $\vert W_k\vert = \displaystyle\prod_{i=1}^{k} (p_{i+1}-1)$ 。
性质 1.2
进一步地，我们也可以得到轮子的筛选效率 $E_k =\large \frac{\vert W_k\vert}{p_k\sharp} = 1 - \displaystyle\prod_{i=0}^{k} \frac{p_{i+1}-1}{p_{i+1}}$
下图即为轮子筛选效率的曲线图。
虽然总体趋势是存在边际效用，但前几个轮子的“费效比”都很好，这启发我们可以用一个比较小的轮子先做粗筛，然后用其他方法做进一步检测。
前面“试除法”检测质数实际就用了 $W_2$ 轮子。
性质 2
轮子上第一个点是 $1$。
从 性质 1 也可以推出，因为在构建新轮子过程中它永远不会被删除；或者根据轮子的定义，$1$ 与任何数互质，所以永远在轮子里。
性质 3
轮子 $W_k$ 上的第二个点是 $p_{k+1}$ 。
首先根据质数分布规律，我们可以确定 $p_{k+1} \lt p_k\sharp$ ，也就是 $p_{k+1} \in W_k$；其次，如果有任何 $x \in W_k$，满足 $1\lt x \lt p_{k+1}$， 那么它就是最小的 $\gt p_k$ 的质数，这就与 $p_{k+1}$ 的定义矛盾了。
性质 4
轮子上的点具有对称性。
如图-轮子所示，轮子上点沿着 $0\degree-180\degree$ 中心轴几何对称。
证明如下：
使用诱导推理，
- 对于 $W_1$ 只有一个 $1$ 在周长为 $p_1=2$ 的圆圈上，对称性成立；
- 假设 $W_k$ 对称性成立，那么由于 $C_{k+1}$ 由 $C_k$ 滚动而成，原来 $C_k$ 上标记的点滚动出的“印记”也因为 $C_k$ 的对称性而对称，而之后删除的“辐条点”也是对称的，所以剩下的“印记”仍然保持对称性，因此 $W_{k+1}$ 对称性也成立。
证毕。
利用对称性，可以构造更节省空间的半轮（semi-wheel），但连 Pritchard 都指出这么做有失优雅、高效。
性质 4.1
每个轮子上最后一个点是 $\vert W \vert - 1$ 。
因为 性质 2 ，每个轮子上第一个点都是 $1$ ，根据对称性有最后一个点是 $\vert W \vert - 1$ 。
轮筛骗局（×）
Pritchard 可能为他的轮筛小发现高兴坏了，竟然昏了头，提出了一个纯轮筛的算法。
他的想法是这样的，既然 $W_k$ 可以直接发现 $\lt p_{k+1}^2$ 范围内的所有质数，那么只要造一个足够大的轮子，使得 $N \lt p_{k+1}^2$，然后让它滚起来，滚到 $N$，是不是就可以解决问题了。10
Pritchard 还引用了他心爱的 $p\cdot f$ 的“乘法改加法”（下面会讲）的算法（负）优化，指出在结合了此等优化的前提下，算法操作的平均时间复杂度可以达到 $\Theta(\frac{N}{\log\log N}) $ 。
样例代码
因为要应付更多的功能，使用了一个比前面 Mairson 筛子更复杂的基于数组的紧凑型双头列表。
/// Sublinear additive sieve by Paul Pritchard
pub fn wheel_sieve(n: usize) -> impl Iterator<Item = usize> {
/// saving 1/3 time compared with vector (each turn create new vector).
///
/// space cost about 3/5 N.
struct CompactDoubleArrayList {
/// 0 for nil
tail: usize,
/// [value, forward, backward]
arr: Vec<Meta>,
}
#[derive(Default)]
struct Meta {
value: usize,
left: usize,
right: usize
}
impl CompactDoubleArrayList {
fn new() -> Self {
let tail = 0;
let arr = vec![Meta::default()];
Self { tail, arr }
}
fn push(&mut self, v: usize) {
self.arr[self.tail].right = self.tail + 1;
let new_node = Meta {
value: v,
left: self.tail,
right: 0
};
if self.tail == self.arr.len() - 1 {
self.arr.push(new_node); // dynamic extend for saving some memory
} else {
self.arr[self.tail + 1] = new_node;
}
self.tail += 1;
}
fn filtering<P: Fn(usize) -> bool>(&mut self, pred: P) {
let mut i = self.arr[0].right;
while i != 0 {
if !pred(self.arr[i].value) {
let left = self.arr[i].left;
let right = self.arr[i].right;
self.arr[left].right = right;
self.arr[right].left = left;
}
i = self.arr[i].right;
}
}
fn nth(&self, index: usize) -> usize {
let mut i = self.arr[0].right;
let mut c = 0;
while i != 0 {
if c == index {
return self.arr[i].value;
}
i = self.arr[i].right;
c += 1;
}
unreachable!("{index} > {c}");
}
fn into_iter(self) -> impl Iterator<Item = usize> {
std::iter::from_coroutine(
#[coroutine]
move || {
let mut i = self.arr[0].right;
while i != 0 {
yield self.arr[i].value;
i = self.arr[i].right;
}
},
)
}
fn rolling(&mut self, l: usize, n: usize) {
let mut i = self.arr[0].right;
debug_assert!(i != 0);
while l + self.arr[i].value <= n {
self.push(l + self.arr[i].value);
i = self.arr[i].right;
}
}
fn delete_multiple_p(&mut self, p: usize) {
self.filtering(|v| v % p != 0)
}
}
std::iter::from_coroutine(
#[coroutine]
move || {
if n < 2 {
return;
}
let mut p = 3usize;
// let mut w = vec![1]; // w_1
let mut w = CompactDoubleArrayList::new();
w.push(1);
let mut l = 2;
yield 2;
while p.pow(2) <= n {
w.rolling(l, min(p * l, n));
w.delete_multiple_p(p);
yield p;
// prevent multiple overflow
l = min(p * l, n);
p = w.nth(1);
}
w.rolling(l, n);
for v in w.into_iter().skip(1) {
yield v;
}
},
)
}
滚动加法构造轮子
尽管算法本身没有意义，但 rolling 作为 Pritchard 心爱的“乘法改加法”的优化之一还要讲一下。
按照图-轮子的思路，把轮子从 $W_k$ 滚动到 $W_{k+1}$ ，可以直接通过 $x = a\cdot p_k\sharp + b,\ a\in 1..(p_{k+1}-1),\ b\in W_k $ 以乘法的形式构建；
但是也可以通过 $x = p_k\sharp + (a-1)\cdot p_k\sharp + b$ 以滚动加法的形式构建。
rolling 实现就是后者，保证选择的值和待插入元素总是差一个 $p_k\sharp$ 身位。
简化的伪代码：
fn rolling {
let mut b = W[0];
while l + W[0] <= n {
W.push(l + next(W, b));
b = next(W, b);
}
}
骗局所在
如果了解轮子性质 1.2 ，那我们可能觉得这种无限制地造大轮子地做法可能有点儿问题；
或者如果了解质数分布规律，并具有一些基本代数的常识，也可能敏锐地察觉出其中的问题。
没错，Pritchard 的纯轮筛隐含了一个假设，那就是 $p_{k+1}^2 \gt p_k\sharp$ ，这才有构造大轮子，再用大轮子滚一些圈，滚到 $N$ 的使用场景。
而实际情况是 $p_{n+1}^2 \sim \frac{(n+1)^2}{\log^2(n+1)}$ 而 $n\sharp = e^{n(1+o(1))} \sim e^n$ ，根据微分知识有
\[\lim_{n\rightarrow\infty} \frac{p_{n+1}^2}{n\sharp} = 0\\\]也就是说，长远看 $p_{k+1}^2$ 是绝对跑不过 $p_k\sharp$ 的，下图是二者的变化曲线
为了方便可视化地比较，图上曲线只取到了 $k=5$ ，事实上后面 $p_{k+1}^2$ 的函数曲线相比于 $p_k\sharp$ 已经近乎为水平线了。
图上可以看出，只在 $k\leqslant 3$ 时才有轮子周长小于它有效筛选范围，之后一个轮子的有效筛选范围远远小于它自身的周长，单就这一点算法就不成立。
更不用说，这种 $e^n$ 的增长速度使得根本没有空间去储存一个完整的轮子。
分段固定轮筛（√√√√）
分段固定轮筛（SFWS，Segmented Fixed-Wheel Sieve）11顾名思义，是在一个固定大小的轮子粗筛后的结果上再做第二步筛选，过程使用了分段技术。
具体思路
设定给定正整数 $N$ ，求取 $\leqslant N$ 范围内所有质数。
首先定义 $p_{np} = \max(\lbrace p \vert\ p^2 \leqslant N \rbrace)$ ，也就说 $\leqslant N$ 范围内的合数最大质因子是第 $np$ 个质数。
假设使用了一个 $W_k$ 的轮筛，那么显然只需要再筛除从第 $k+1$ 到第 $np$ 个质因子构成的合数就可以完成质数筛选。
令 $c = p \cdot f \leqslant N,\ (p\in p_{k+1}..p_{np})$ ，在“粗筛”的结果上选取 $f \in W_k^*$ （这一步过程仍然利用粗筛的结果），将这些 $c$ 标记为非质数。
过程采取分段技术并没有让任何东西变得复杂。
计算 $np$
假如取分片大小 $\Delta = \lfloor\sqrt {N}\rfloor $ ，计算 $ \leqslant \Delta$ 的所有质数，于是有 $\max^2 \lbrace p \leqslant \Delta \rbrace \leqslant \Delta^2 \leqslant N $ 。
显然有 $\max \lbrace p \leqslant \Delta \rbrace = p_{np}$ ，即 $np = \vert \lbrace p \leqslant \Delta \rbrace \vert$ 。
反证法证明，如果存在 $p_{np} \gt \Delta$ ，那么 $\lfloor\sqrt {N}\rfloor \geqslant p_{np} \gt \Delta$ ，这就与 $\Delta$ 的定义自相矛盾了。
预备轮子
一个 $W_7$ 的固定轮子就够大了，$\vert W_7 \vert = \displaystyle\prod_{i=1}^{7} p_i = 510,510$ ，光空间占用就已经有 4 MB 了。
轮子的计算可以参考前面章节滚动加法构造轮子，过程中可以顺便构造轮子 $W$ 的增量表示 $\textit{WG}$
\[\textit{WG}[i] = W^*[i+1] - W^*[i], \quad 0 \leqslant i \leqslant |W|-1\]引导程序
如上所述，SFWS 需要先计算一个$ \Delta$ 范围内的质数，推荐直接使用简单的 Eratosthenes 筛子 。
当然也可以“自举”，只是效能差一点点。
递归调用就要设置结束条件，可以设置当 $N \lt p_{k+1}^2$ 时，直接通过滚动轮子计算出所有目标质数。
但是轮子无法计算 $0..(p_{k+1}-1)$ 范围内的质数，仍然需要预先计算 $p_1 .. p_k$ 。
// bootstrapping
for i in 1..=k {
if P[i] > n {
return;
}
yield P[i];
}
let mut v = 1 + wg[0];
let mut vi = 1;
if n < w[1] * w[1] {
while v <= n {
yield v;
v += wg[vi];
vi = (vi + 1) % wg.len();
}
return;
}
let delta = n.isqrt();
let pris = fixed_wheel_seg_sieve(delta).collect::<Vec<usize>>();
样例代码
pub fn fixed_wheel_seg_sieve(n: usize) -> impl Iterator<Item = usize> {
let k = 7;
let WStruct {
wheel: w,
wheel_gap: wg,
prod,
// ipm,
..
} = &W[k];
std::iter::from_coroutine(
#[coroutine]
move || {
if n == 0 {
return;
}
let delta = n.isqrt();
let pris = e_sieve(delta).collect::<Vec<usize>>();
let np = pris.len();
let mut v = 1 + wg[0];
let mut vi = 1;
if np <= k {
// Just rolling to n
for i in 1..=k {
if P[i] > n {
return;
}
yield P[i];
}
while v <= n {
yield v;
v += wg[vi];
vi = (vi + 1) % wg.len();
}
return;
}
for i in 0..pris.len() {
yield pris[i];
}
/* Init v0, vi */
let v_raw = delta + 1;
let (mut v, mut vi) = locate_in_wheel(w, *prod, v_raw);
/* Init factors */
// absolute value
let mut factors = vec![];
for i in 0..np - k {
let p = pris[k + i];
// (delta + p - delta % p) + 1
let f_raw = delta / p + 1;
factors.push(locate_in_wheel(w, *prod, f_raw));
}
/* Run the algorithm */
let mut bits = BitVec::from_elem(delta + 1, true);
for l in (delta..=n).step_by(delta) {
let end = min(l + delta, n);
/* sift for p_k..p_np */
for i in 0..np - k {
let p = pris[k + i];
let (mut f, mut fi) = factors[i];
// let (mut c, mut j) = factors[i];
while p * f <= end {
bits.set(p * f - l, false);
f += wg[fi];
// c += pms[i][wg[j] / 2];
fi = (fi + 1) % wg.len();
}
factors[i] = (f, fi);
// factors[i] = (c, j);
}
/* accumulate primes */
while v <= end {
if bits[v - l] {
yield v;
}
v += wg[vi];
vi = (vi + 1) % wg.len();
}
/* reset for next segment */
bits.set_all();
}
},
)
}
fn locate_in_wheel(w: &[usize], prod: usize, raw: usize) -> (usize, usize) {
let prod_rem = raw % prod;
let prod_base = raw - prod_rem;
let (v0, vi) = match w.binary_search(&prod_rem) {
Ok(i) => (w[i], i),
Err(i) => (w[i], i),
};
(prod_base + v0, vi)
}
在 $W^*$ 上的定位 $v$ 和 $f$
$v \in W^*$ 是轮子滚到每个分段上时第一个点的位置，$vi$ 是 $v \mod p_k\sharp$ 在 $W$ 上的编号。
$f_{p_i}$ 是轮子滚在每个分段上时第一个 $c = p \cdot f$ ，对应 $p_i$ 的 $f$，$fi$ 是 $f \mod p_k\sharp$ 在 $W$ 上的编号。
在 $W^*$ 上的定位 $v$ 和 $f$ 的原理是一样的，不妨就以 $v$ 为例做介绍：
先计算了模 $\vert W \vert$ 的余数 $\textit{prod_rem}$ 和轮子周长整数倍的轨迹长度 $\textit{prod_base}$ ：
let v_raw: usize = l + 1;
let prod_rem = v_raw % prod;
let prod_base = v_raw - prod_rem;
然后直接在 $W$ 上做二分查找，找到第一个 $ \geqslant \textit{prod_rem}$ 的值作为 $v$ 的初始值（$模\vert W \vert$ ）：
因为 $1, \vert W \vert-1 \in W$ ，所以不存在余数 $ \textit{prod_rem}$ 落在轮子外的情况
let (v0, vi) = match w.binary_search(&prod_rem) {
Ok(i) => (w[i], i),
Err(i) => (w[i], i), // prod-1 is prime
};
补上轨迹长度 $\textit{prod_base}$ 得到 $v$ 完整初始值：
let mut v = prod_base + v0;
对计算 $p\cdot f$ 的“优化”
来了，Pritchard 心爱的“乘法改加法”的优化之二，$p\cdot f$ 的“乘法改加法”。
原理是轮子上两个点的距离 $\textit{WG}[i] = \Delta f$ 的值域比较小，可以为轮子计算一个 $\lbrace \textit{WG}[i] \rbrace$ ，这样对于每个 $p$ 也可以预计算一个 $p\cdot \Delta f = \Delta (p\cdot f)$ 。
这样 $p\cdot f = (p\cdot f)’ + \Delta (p\cdot f)$ ，就可以实现乘法改加法。
除此之外，可以观察到 $\textit{WG}[i]$ 总是偶数，利用这个性质可以节约一半的预计算值的存储空间。
但是显见地在代码里我们没用这个优化，因为在付出了代码复杂化、空间占用地代价后，得到了一个更慢的时间性能上的表现。12
复杂度分析
时间复杂度 $O(N)$ ，空间复杂度 $O(\sqrt{N})$ 。
算法评价
虽然经常吐槽 Pritchard ，但他搞的 SFWS 思路还是对的，是我目前为止最推崇的一款筛子，是时间性能和空间性能的双料冠军！
算法外延
按照分段固定轮筛的模式，抽象出 $(\Delta,k)$ 的参数二元组，可以把很多筛子算法归类进来。
详见原文
Mairson 对偶筛（√√√）
Mairson 对偶筛13，对偶（dual）意指把原来算法外层对 $p$ 的遍历和内层对 $f$ 的遍历对调，变成外层对 $f$ 遍历内层对 $p$ 遍历。14
基于最小质因数分解，$c = \texttt{lpf}(c) \cdot f$ 做筛选。
外层 $f$ 是连续的正整数，在 $2..\lfloor\frac{N}{2}\rfloor $ 上迭代；
内层 $p$ 是质数，在 $p_1 .. \texttt{lpf}(f)$ 上迭代 。
样例代码
pub fn mairson_dual_sieve(n: usize) -> Box<dyn Iterator<Item = usize>> {
sieve_spec_case!(n ; [0, 1]);
let mut bits = BitVec::from_elem(n + 1, true);
let mut pris = vec![];
for f in 2..=n / 2 {
if bits[f] {
pris.push(f);
}
for p in pris.iter() {
if f * p > n {
break;
}
bits.set(f * p, false);
// if f % p == 0 {
// break;
// }
}
}
Box::new(
pris.into_iter().chain(
bits.into_iter().enumerate().skip(n / 2 + 1).flat_map(
|(i, flag)| {
if flag {
Some(i)
} else {
None
}
},
),
),
)
}
边缘情况
因为外循环 $f$ 从 $2$ 开始，因此 $N \lt 2$ 的情况需要特别处理。
质数判断
如果发现 $f$ 未被标记，则它一定是质数。
使用反证法，假如它不是质数，那么它一定可以表示为 $f = p \cdot f’$ ，而 $f’ \lt f$ ，那么 $f$ 一定会被标记，这就与前提矛盾了。
质数迭代
如果从最小的质数开始增序迭代，直到第一个能整除 $f$ 的质数，这就是所有 $\leqslant \texttt{lpf}(f)$ 的质数。
但是另一方面我们其实注解了检测整除的代码，这是因为相对于乘法和加法，除法还是一种代价较高的算术运算，提前跳出的好处比不上一直做取余检测的代价，注掉代码不影响正确性却会使得性能获得可察觉的改善。15
算法变种
这个算法更大的价值可能在于它的副产品，最小质因子数组 $\texttt{lpf}$，以用来做质因数分解。
/// 一鱼两吃，既返回值质数列表，也返回质因数分解列表 (lpf)
/// 这种 API 风格倒也正好是 Rust 推荐的风格
pub fn mairson_dual_sieve_factorization(n: usize) -> (Vec<usize>, Vec<usize>) {
let mut lpf = vec![0; n+1];
let mut pris = vec![];
if n < 2 {
return (pris, lpf);
}
for f in 2..=n / 2 {
if lpf[f] == 0 {
lpf[f] = f;
pris.push(f);
}
for p in pris.iter().cloned() {
if p * f > n {
break;
}
lpf[p * f] = p;
if p == lpf[f] {
break;
}
}
}
for i in (n / 2) + 1..=n {
if lpf[i] == 0 {
lpf[i] = i;
pris.push(i);
}
}
(pris, lpf)
}
此时为了 $\texttt{lpf}$ 的正确性，必须严格限制 $p$ 在超过 $f$ 的最小质因子时退出，不过有了 $\texttt{lpf}$ 也省去了取余的代价。
复杂度分析
显见内外层的时间复杂度均为 $O(\sqrt N)$ ，因此总时间复杂度为 $O(N)$ 。
空间复杂度 $O(N)$ 。
算法评价
原始算法时间性能也非常好，比 Eratosthenes 筛子快一点，比 Sundram 筛子慢一点。
变种算法也即 cp-algorithms 里介绍的线性筛子算法，在算法比较的结论上没有变化，但比原始算法要快。16
GPF 筛子（√√）
GPF 筛子13，是基于最大质因数分解， $c = f\cdot \texttt{gpf(c)}$ 的质数筛子。
从最小的质数 $p = 2$ 开始，收集所有使得 $ f \cdot p \leqslant N$ ，并且 $\texttt{gpf}(f) \leqslant p$ 的 $f$ ，划掉对应的 $c = f \cdot p$ ，最后得到质数。
pub fn gpf_sieve(n: usize) -> Box<dyn Iterator<Item = usize>> {
sieve_spec_case!(n; [0, 3]);
let mut p = 2;
let mut bits = BitVec::from_elem(n + 1, true);
let mut factors = vec![];
let mut i = 2;
let mut pris = vec![];
while p <= n / 2 {
pris.push(p);
factors.push(p);
let mut f_stack = factors;
factors = vec![];
while let Some(f) = f_stack.pop() {
if p * f <= n {
bits.set(p * f, false);
f_stack.push(p * f);
factors.push(f);
}
}
i += 1;
while !bits[i] {
i += 1
}
p = i;
}
Box::new(
pris.into_iter().chain(
bits.into_iter()
.enumerate()
.skip(n / 2 + 1)
.filter_map(|(i, flag)| if flag { Some(i) } else { None }),
),
)
}
边缘情况
因为外循环从 $p=2\leqslant \lfloor \frac{N}{2}\rfloor$ 开始， ，因此 $N \lt 4$ 的情况需要特别处理。
复杂度分析
由于每个 $c$ 只会被计算一次，因此时间复杂度可被认为是 $O(N)$ 。
空间复杂度为 $O(N)$ 。
算法评价
时间性能还算可以，比分段 Eratosthenes 筛慢一点。
Atkin 筛子（?）
Atkin 筛子17，是一种二元二次型筛子。
它的思路还是挺先进的，先用一个 2-3-5 筛子在模 60 的余数上，得到
\[\lbrace 1,7,11,13,17,19,23,29,31,37,41,43,47,49,53,59 \rbrace\]然后在这些余数上，可以分别应用三个二元二次方程，通过解数量的奇偶性做进一步筛选（要求奇数个解）；
最后做质数平方因子的检查（确保 squarefree）完成质数确认。
方程-1
对于 $\delta \in \lbrace 1, 13, 17, 29, 37, 41, 49, 53 \rbrace$ ，执行 $ 4x^2 + y^2 = 60k + \delta \equiv 1 \mod 4$ 。
方程-2
对于 $\delta \in \lbrace 1, 7, 13, 19, 31, 37, 43, 49 \rbrace$ ，执行 $ 3x^2 + y^2 = 60k + \delta \equiv 1 \mod 6$ 。
为了不和方程-1检查的范围重叠，可以只检查在 $\delta \in \lbrace 7,19,31,43 \rbrace$ ，也就是 $7 \mod 12$ 。
方程-3
对于 $\delta \in \lbrace 11, 23, 47, 59 \rbrace$ ，执行 $ 3x^2 - y^2 = 60k + \delta \equiv 11 \mod 12$ 。
一点解释
首先，这三个方程里的 $(x, y)$ ，就像 Sundaram 筛子 一样，都是实在的正整数；
其次，为什么是这三个方程，为什么是奇数个解，为什么方程-3要求 $x \gt y$，为什么还要校验不含质数平方因子，原文里有解释18 。
原始实现（×）
原始论文的主要价值在于（宣称）突破了 Pritchard 的质数筛子算法空间复杂度和时间复杂度不能同时为亚线性的猜想，提出了一种理论分析在时间复杂度为 $O(\large\frac{N}{\log\log N})$ ，而空间复杂度为 $O(\sqrt N)$ 的新算法。
但这是一种诈骗，因为：
- 实际上根本不可能在规定时间复杂度内枚举完任意一个方程的解，而且按照论文里对方程-3解的枚举算法根本就是错的，不能枚举全部符合条件的解；
- 检查质数平方因子也无法同时满足亚线性的时间和空间复杂度。
但无论如何，我们试着按照原文的思路实现了一版出来。
样例代码
mod atkin {
use std::cmp::min;
use lazy_static::lazy_static;
pub(super) fn algs1(x: usize, y: usize) -> usize {
4 * x * x + y * y
}
pub(super) fn algs2(x: usize, y: usize) -> usize {
3 * x * x + y * y
}
pub(super) fn enable_algs3(x: usize, y: usize) -> bool {
x > y
}
pub(super) fn algs3(x: usize, y: usize) -> usize {
3 * x * x - y * y
}
lazy_static! {
pub(super) static ref DELTA16: [usize; 16] =
[1, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 49, 53, 59];
// {1,13,17,29,37,41,49,53}
pub(super) static ref DELTA16_ALGS1: [usize; 8] =
[0, 3, 4, 7, 9, 10, 13, 14];
// trim duplicated delta number campared with 1
// {7,19,31,43}
pub(super) static ref DELTA16_ALGS2: [usize; 4] =
[1, 5, 8, 11];
// {11, 23, 47, 59}
pub(super) static ref DELTA16_ALGS3: [usize; 4] =
[2, 6, 12, 15];
pub(super) static ref DELTA16_GRPS: Vec<Vec<(usize, usize)>> = {
let mut delta16_grps: Vec<Vec<(usize, usize)>> = vec![vec![]; 16];
/* algorithm 1. 4x^2 + y^2 = n */
for i in DELTA16_ALGS1.iter().cloned() {
for f in 1..=15 {
for g in 1..=30 {
if algs1(f, g) < DELTA16[i] {
continue;
}
if (algs1(f, g) - DELTA16[i]) % 60 == 0 {
delta16_grps[i].push((f, g));
}
}
}
}
/* algorithm 2. 3x^2 + y^2 = n */
for i in DELTA16_ALGS2.iter().cloned() {
for f in 1..=15 {
for g in 1..=30 {
if algs2(f, g) < DELTA16[i] {
continue;
}
if (algs2(f, g) - DELTA16[i]) % 60 == 0 {
delta16_grps[i].push((f, g));
}
}
}
}
/* algorithm 3. 3x^2 - y^2 = 60k + delta */
// FIXME: incorrect algoriuthm
for i in DELTA16_ALGS3.iter().cloned() {
for f in 3..=10 {
for g in 1..=min(30, f-1) {
if algs3(f, g) < DELTA16[i] {
continue;
}
if (algs3(f, g) - DELTA16[i]) % 60 == 0 {
delta16_grps[i].push((f, g));
}
}
}
}
delta16_grps
};
}
}
pub fn atkin_sieve_enum_lattice(n: usize) -> impl Iterator<Item = usize> {
use atkin::*;
std::iter::from_coroutine(
#[coroutine]
move || {
// P[17] = 59
for i in 1..=17 {
if P[i] > n {
return;
}
yield P[i]
}
if n == 59 {
return;
}
let n_k = n.div_ceil(60);
let delta_k = (n_k - 1).isqrt();
let delta = delta_k * 60;
let mut bits_k = BitVec::from_elem(delta_k * 16, false);
let mut pri_square = HashSet::<usize>::new();
for i in 1..=17 {
let r = P[i] * P[i];
for j in (r..=n).step_by(r) {
pri_square.insert(j);
}
}
let mut l = 60;
let mut l_k = 1;
while l <= n {
/* algorithm 1 4x^2 + y^2 = n */
for i in DELTA16_ALGS1.iter().cloned() {
let mut pairs = HashSet::<(usize, usize)>::new();
for (f, g) in DELTA16_GRPS[i].iter().cloned() {
let mut x = f;
let mut y0 = g;
let mut k0 = (algs1(f, g) - DELTA16[i]) / 60;
while k0 < l_k + delta_k {
k0 += 2 * x + 15;
x += 15;
}
while x > 15 {
x -= 15;
k0 -= 2 * x + 15;
while k0 < l_k {
k0 += y0 + 15;
y0 += 30;
}
let mut k = k0;
let mut y = y0;
while k < l_k + delta_k {
if pairs.insert((x, y)) {
let bi = (k - l_k) * 16 + i;
bits_k.set(bi, !bits_k.get(bi).unwrap());
}
k += y + 15;
y += 30;
}
}
}
}
/* algorithm 2 3x^2 + y^2 = n */
for i in DELTA16_ALGS2.iter().cloned() {
let mut pairs = HashSet::<(usize, usize)>::new();
for (f, g) in DELTA16_GRPS[i].iter().cloned() {
let mut x = f;
let mut y0 = g;
let mut k0 =
((algs2(f, g) - DELTA16[i]) / 60) as isize;
while k0 < 0 || (k0 as usize) < l_k + delta_k {
k0 += (x + 5) as isize;
x += 10;
}
while x > 10 {
x -= 10;
k0 -= (x + 5) as isize;
while k0 < 0 || (k0 as usize) < l_k {
k0 += (y0 + 15) as isize;
y0 += 30;
}
let mut k = k0;
let mut y = y0;
while (k as usize) < l_k + delta_k {
if pairs.insert((x, y)) {
let bi = (k as usize - l_k) * 16 + i;
bits_k.set(bi, !bits_k.get(bi).unwrap());
}
k += (y + 15) as isize;
y += 30;
}
}
}
}
/* algorithm 3 3x^2 - y^2 = 60k + delta */
/* NOTE: There is a bug for origin formula-3
enumerate lattice point */
for i in DELTA16_ALGS3.iter().cloned() {
// let mut pairs = HashSet::<(usize, usize)>::new();
for k in l_k..l_k + delta_k {
let c = 60 * k + DELTA16[i];
for x in isqrt_ceil!((c + 1) / 3)..=n.isqrt() {
let y2 = 3 * x * x - c;
let y = (3 * x * x - c).isqrt();
if y * y == y2 && y < x {
let bi = (k as usize - l_k) * 16 + i;
bits_k.set(bi, !bits_k.get(bi).unwrap());
}
}
}
}
/* remove p^2 */
for k in l_k..l_k + delta_k {
for i in 0..16 {
if bits_k[(k - l_k) * 16 + i] {
let c = 60 * k + DELTA16[i];
if c > n {
break;
}
if !pri_square.remove(&c) {
yield c;
let r = c * c;
for j in (r..=n).step_by(r) {
pri_square.insert(j);
}
}
}
}
}
/* update */
bits_k.clear();
l += delta;
l_k += delta_k;
}
}
)
}
算法评价
仅正确，性能上实际不可用。
简单实现（√√）
除了原始版本外，还有一个不知道为何在网上广泛流传的简单实现版本，它直接遍历了所有二元组，先为三个方程计算值，反过来通过余数进行筛选。
相对于原始实现，它是一个可以接受的算法（实现），但这样时间复杂度和空间复杂度都成了 $O(N)$ 。
样例代码
pub fn atkin_sieve_simple(n: usize) -> impl Iterator<Item = usize> {
use atkin::*;
std::iter::from_coroutine(
#[coroutine]
move || {
let mut bits = BitVec::from_elem(n + 1, false);
if n > 1 {
bits.set(2, true);
}
if n > 2 {
bits.set(3, true);
}
for x in 1..=n.isqrt() {
for y in 1..=n.isqrt() {
let c1 = algs1(x, y);
// not using 2-3-5 wheel sieve for efficiency
if c1 <= n && (c1 % 12 == 1 || c1 % 12 == 5) {
bits.set(c1, !bits[c1]);
}
let c2 = algs2(x, y);
// 1 mod 6 => 7 mod 12
// trim duplicate element with algs1
if c2 <= n && c2 % 12 == 7 {
bits.set(c2, !bits[c2]);
}
if enable_algs3(x, y) {
let c3 = algs3(x, y);
if c3 <= n && c3 % 12 == 11 {
bits.set(c3, !bits[c3]);
}
}
}
}
/* trim p^2 */
for i in 5..=n.isqrt() {
if bits[i] {
let r = i * i;
for j in (r..=n).step_by(r) {
bits.set(j, false);
}
}
}
for i in 1..=n {
if bits[i] {
yield i;
}
}
},
)
}
算法评价
速度很快算是第二档，但本身既无法分片又不如 Eratosthenes 筛子那么简单直观，这就使得它实际没有任何可提之处，权列在此，以为参考。19
尾声
注解
-
G. H. Hardy and E. M. Wright. An Introduction to the Theory of Numbers. 1962. ↩
-
从另一方面说，在 CPython 上的实现倒还能体现这种优化的作用 ↩
-
Harry G. Mairson. Some new upper bounds on the generation of prime numbers. 1977. ↩
-
J.Misra. An Exercise in Program Explanation. 1979. ↩
-
形式地说，任意两个相邻的最小质因数为 $p_i$ 的自然数之间，至少存在一个最小质因数为 $p_j \gt p_i$ 的自然数。 ↩
-
Paul Pritchard. A Sublinear Additive Sieve for Finding Prime Numbers. 1981. ↩
-
这里使用 量词 $k$ 而不是上下文惯用的 $n$ 有两方面考虑，一方面是和 Explaining the Wheel Sieve 原文的用法保持一致；另一方面 有些终结的意味的 $n$ ，$k$ 是更能暗示处于中间过程的一个“量词”，在轮子上和质数阶乘上使用更合适。 ↩
-
这简直就是经典科幻小说家会干的事 ↩
-
Paul Pritchard. Fast Compact Prime Number Sieves (among Others). 1983. ↩
-
在 CPython 上的实现只在很大的轮子上和很大的输入数据的规模上有微弱优势 ↩
-
Paul Pritchard. LINEAR PRIME-NUMBER SIEVES: A FAMILY TREE. 1987. ↩ ↩2
-
原文作者会为每个既有算法考虑它的对偶算法 ↩
-
在 CPython 上的实现如果留着这段代码反而会带来显著的性能提升，这几乎反向明示了 CPython 并没有对乘法有什么优化 ↩
-
在 CPython 上的实现也同意这个结论 ↩
-
A. O. L. Atkin and D. J. Bernstein. Prime Sieves Using Binary Quadratic Forms. 2003. ↩
-
但它使用了我不熟悉的数学工具（抽象代数等），所不了解的数学知识（数论），而且写得看起来也并不打算真的想让人了解。 ↩
-
并且因为包含过多的算术运算，在 CPython 上的实现非常低效 ↩
-
这个论文里数学符号的排版字体真的抽象，首先这个字符
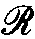是什么？ 版上打眼一看都缩缩成一团了，还以为是个花体 $A$ 呢，仔细看不是，难道是什么大写希腊字母的花体么，因为拜占庭作为中世纪西方数学教育翻译的主要材料来源地之一，使得作为传统，西方人写数学符号都好整个希腊字母，但仔细对了一遍也不像，后来通过谷歌识图对比类似结果，算是确认这是个 $R$ 。 如果提前知道它是个 $R$ ，那它看起来还挺像个 $R$ 的，可这个字符
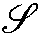又是什么？它看起来像 $y$ 又像 $g$ ，这下谷歌识图也识不出来了，只能在专门的字体网站做 AI 识图，然后发现这居然是个 $S$ ，S 它是你么，它说它舅（就) 是我。这个字体名叫 OriginalScriptStd ，英文草书说是。 ↩
