BST(2) - RB(0) - 原始红黑树

Algorithm

January 19, 2023

基本概念

红黑树是一种对平衡的要求比前面介绍的 AVL树 宽松一些的自平衡二叉搜索树，因此虽然查询性能稍差，但有更少的插/删所需要的旋转次数，也就是写的性能更加优秀。它是在在 1978 年由 Leonidas J. Guibas and Robert Sedgewick 联合提出，用红黑色标识区分主要是考虑到排版系统和手写方面的好处。（它模仿了 $4$ 阶 B树）

红黑树把节点分为红色和黑色（空节点视为黑色），规定新增的节点都是红色，而红色节点的父节点不能也是红色节点，在这种情况下保持每个节点的所有叶子节点到该节点的路径上黑色结点数相等，或者简称黑高相等，这样就能保持树的平衡性。另外应该是出于减少不必要重平衡的操作，特别规定根节点应设为黑色。

在红色节点不能连续的情况下，如果黑高相等，那意味着最大的树高的差距不超过 $1$ 倍。

系列展望

红黑树，由于一些历史原因很流行，在工程领域有众多的应用，在学术领域衍生出了很多变种。比如 Linux 上的 CFS（ Completely Fair Scheduler）任务调度系统、系统调用 epoll 的实现，Java 8 的 HashMap 里组织哈希碰撞的元素用了红黑树代替链表，很多旧的 TreeMap 实现也都是红黑树的变种。在后面会介绍几个有名的红黑树变种。

然而可以保证，不管是类比 2-4 树还是学习了前面的红黑树（或变种）对于后面的红黑树变种在实现上的理解没有任何帮助。归根结底红黑树就不是一个和我们之前或之后介绍的所有自平衡二叉树那样概念很清楚，实现很简单的一个东西，它的红黑约束一方面记录了平衡关系，从而可以确认重平衡开始的时机；另一方面又需要维护这种红黑约束，阻碍了重平衡的实现，除了节点上的红黑元数据可以压缩到 1 bit 然后嵌入其他数据里，从而实现 0 cost 存储，实在找不到其它特别的优点，而在现代存储计算机系统里面已经不需要那么极限地节省内存，在这种情况下红黑树完全不如 B+ 树。

特别地，在删除节点的时候，如果被删节点左右子树都不为空的时候，对红黑约束的修复非常困难，这导致几乎所有的实现都在使用一个非常 Tricky 的方法：假交换，来规避这种过于复杂的情况，使得可以只处理一个孩子为空的情况，（但即使这样仍然相当复杂）。

假交换

比起通过旋转改变节点间的实际的引用关系，假交换是仅仅交换节点实际内容： key 和 val 字段，而不改变引用关系，这样可以规避对复杂节点关系的处理。

但是正如它所做的事情客观的展示那样，假交换非常的不体面，它彻底破坏了节点引用与键值对的固定关系，引入了潜在的 Bug （比如你可能保存了之前查询到的某个节点的引用，然后对另外节点进行操作时，意外地发现之前持有的节点的 key， val 字段也发生了改变）

我个人是非常非常不喜欢这种糟糕的 tricky 的方式，但整个红黑树系列操作的基础就是这种不体面的假交换，所以我说这个红黑树算法就很怪。

macro_rules! swap {
    (node | $x:expr, $y:expr, $attr:ident) => {
        {
            let x = $x.clone();
            let y = $y.clone();

            let x_attr = attr!(x, $attr);
            let y_attr = attr!(y, $attr);

            attr!(x, $attr, y_attr);
            attr!(y, $attr, x_attr);
        }
    };
}

/// Used in red-balck tree serials
///
/// Trciky method
macro_rules! fake_swap {
    ($x:expr, $y:expr) => {
        {
            let x = $x.clone();
            let y = $y.clone();

            swap!(node| x, y, key);
            swap!(node| x, y, val);
        }
    };
}

基础定义

共同结构

impl_node!();
impl_node_!({ color: Color });
impl_tree!(RB {});

impl<K: Debug, V> Debug for Node<K, V> {
    fn fmt(&self, f: &mut std::fmt::Formatter<'_>) -> std::fmt::Result {
        if self.is_some() {
            write!(f, "{:?}({:?})", key!(self), self.color())
        } else {
            write!(f, "nil({:?})", self.color())
        }
    }
}

专属辅助

impl<K, V> Node<K, V> {

    ////////////////////////////////////////////////////////////////////////////
    /// Static Stats

    #[inline]
    fn color(&self) -> Color {
        if self.is_none() {
            Black
        }
        else {
            color!(self)
        }
    }

    #[inline]
    fn is_red(&self) -> bool {
        self.color().is_red()
    }

    #[inline]
    fn is_black(&self) -> bool {
        self.color().is_black()
    }

    #[inline]
    fn color_flip(&mut self) {
        debug_assert!(self.is_some(), "Color flip on None");

        color!(self, self.color().rev())
    }
}

平衡校验

impl_balance_validation!(RB ->
    #[cfg(test)]
    fn balance_validation(&mut self) {
        self.root.validate_rb_rule();
        self.root.validate_black_balance();
    }
);


impl<K, V> Node<K, V> {
    ////////////////////////////////////////////////////////////////////////////
    /// Validation Helper

    #[cfg(test)]
    fn validate_rb_rule(&self) {
        if self.is_none() {
            return;
        }

        if self.is_red() {
            assert!(paren!(self).upgrade().is_black())
        }

        left!(self).validate_rb_rule();
        right!(self).validate_rb_rule();
    }

    /// 应该给每个节点校验，但是存储黑高是一个问题，单独搞一个数据结构又太费
    /// 于是多次总体校验的方式
    #[cfg(test)]
    fn validate_black_balance(&self) {
        if self.is_none() {
            return;
        }

        use itertools::Itertools;

        let is_black_blance =
        self
            .leaves()
            .into_iter()
            .map(|x| x.black_depth_to(self))
            .tuples()
            .all(|(a, b)| a == b);

        assert!(is_black_blance);
    }

    #[cfg(test)]
    fn black_depth_to(&self, end: &Self) -> usize {
        let mut depth = 0;
        let mut p = self.clone();

        while p.is_some() && !p.rc_eq(end) {
            if p.is_black() {
                depth += 1;
            }

            p = paren!(p).upgrade();
        }

        depth
    }

    /// store paren for nil leaf
    #[cfg(test)]
    fn leaves(&self) -> Vec<Self>
    where K: Debug
    {
        let mut leaves = vec![];

        if self.is_none() {
            return leaves;
        }

        let mut q = crate::vecdeq![self.clone()];

        while let Some(x) = q.pop_front() {
            let left = left!(x);
            let right = right!(x);

            // 两片本质一样的叶子只保留其中一页
            if left.is_none() || right.is_none() {
                leaves.push(x.clone());
            }

            if left.is_some() {
                q.push_back(left);
            }

            if right.is_some() {
                q.push_back(right!(x));
            }
        }

        leaves
    }

}

重平衡

在介绍具体的重平衡事务之前，先强调一下对于红黑树而言，旋转结束要额外交换新旧根的颜色。

impl_rotate_cleanup!(RB ->
    fn rotate_cleanup(&self, x: Node<K, V>, z: Node<K, V>) {
        /* swap color */
        if x.is_some() && z.is_some() {
            swap!(node | x, z, color);
        }
        else {
            debug_assert!(x.is_black() && z.is_black());
        }
    }
);

插入重平衡

插入思路来源于 brilliant.org 相关页面

插入节点后的重平衡是比较容易的，无非是如何处理新增节点导致的 红违背（red violation），也就是父子两个节点都是红色节点的情况。

这时主要有三种情况：

假设插入的红节点为 $\texttt{i}$ ，$\texttt{i}$ 的父节点为 $\texttt{p}$ ， $\texttt{p}$ 的父节点为 $\texttt{pp}$ ， $\texttt{p}$ 的邻居节点是 $\texttt{psib}$

case-1

$\texttt{psib}$ 是红节点，只需要把 $\texttt{pp}$ , $\texttt{p}$ , $\texttt{psib}$ 反色，并一路向上修复（递归地解决问题），这样既修复了红违背又保持了黑平衡

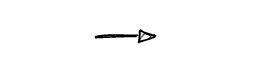
case-2

$\texttt{psib}$ 是黑节点，并且 $\texttt{p} \rightarrow \texttt{i}$ 的方向与 $\texttt{pp} \rightarrow \texttt{p}$ 的方向相反，向 $\texttt{p} \rightarrow \texttt{i}$ 的反方向旋转，到 case-3

case-3

$\texttt{psib}$ 是黑节点，并且 $\texttt{p} \rightarrow \texttt{i}$ 的方向与 $\texttt{pp} \rightarrow \texttt{p}$ 的方向相同，向 $\texttt{p} \rightarrow \texttt{i}$ 的反方向旋转，并且把 $\texttt{p}$ 和 $\texttt{pp}$ 反色

case-2 可以直接双旋，然后反色一步到位地解决

/// impl RB

pub fn insert(&mut self, k: K, v: V) -> Option<V>
{
    let color;

    if self.root.is_none() {
        color = Black;
    }
    else {
        color = Red;
    }

    let z = node!( BST { k, v, color: color });

    let popped = bst_insert!(self, z.clone());

    self.fix_red_violation(z);

    popped
}


fn fix_red_violation(&mut self, ent: Node<K, V>)
{
    let mut i = ent;
    let p = paren!(i).upgrade();

    if p.is_black() { return }

    /* Both p and pp is RED */

    let pp = paren!(p).upgrade();
    let red_dir = index_of_child!(p, i);
    let p_dir = index_of_child!(pp, p);
    let psib_dir = p_dir.rev();

    let psib = child!(pp, psib_dir);

    /* case-1 */

    if psib.is_black() {
        if p_dir == red_dir {
            /* case-3 */
            rotate!(self, pp, psib_dir);
        }
        else {
            /* case-2 */
            double_rotate!(self, pp, psib_dir);
        }
    }
    else {  // psib is red
        p.color_flip();
        psib.color_flip();

        if !pp.rc_eq(&self.root) {
            pp.color_flip();
            self.fix_red_violation(pp);
        }
    }
}

// impl ...

合法的颜色关系

在介绍仍然相当复杂的删除重平衡之前，作为一个基础，先认识一下符合红约束和黑平衡条件下的“合法“的颜色关系。

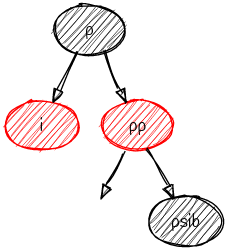
假设父节点 $\texttt{p}$ 和它的两个孩子 $\texttt{c}_0$ , $\texttt{c}_1$ ：

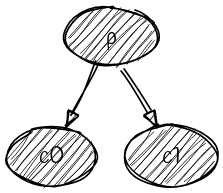
$P$	$C_0$	$C_1$
Red	Black	Black
Black	Black	Black
Black	Red	Red
Black	nil (or Red)	Red (or nil)

借助这个关系列表，可以提高我们对红与黑的理解：

红色表示约束，只要有一个节点是红色，那它的左右孩子和父母的颜色就都是确定的了（都是黑色）；而黑色是无所谓的，没有约束的，一个黑色节点的孩子可以是任意颜色。

反过来从删除的角度讲，可以随意删除一个红色节点，而黑色节点则需要进行调整。

另外我们还发现当黑色节点的一个孩子是红色另一个孩子是黑色时，这个黑孩子一定是 $\texttt{nil}$ 节点，否则就会黑失衡。

在讨论红黑树平衡的情况时，nil 节点也在考虑的范围内，同时它在其他地方又沿用传统上非nil叶子节点的定义，这是红黑树自己的问题。

删除重平衡

删除来源于和 en.wiki 相关页面

在介绍删除重平衡之前有必要先介绍以下删除操作：

使用假交换确保被删除的节点至少有一个孩子是空的；
（优先）用非空的孩子替换被删除的节点。

假设被删节点是 $\texttt{z}$ ，替换它的子节点是 $\texttt{child}$

如果 $\texttt{z}$ 是红色，或者 $\texttt{child}$ 是红色（此时只需把 $\texttt{child}$ 染黑），那删除操作不会造成对黑平衡的破坏；

但如果 $\texttt{z}$ 是黑色， $\texttt{child}$ 也是黑色（包括 NIL 节点），除非 $\texttt{z}$ 是根节点，否则，以它为根的子树的黑高就会少 $1$ ，有的地方把这种 黑失衡 的情况称为 double black ，因为好像是两个黑节点被压到了一个节点上。

删除操作的情况如下所示：

// impl RB

pub fn remove<Q>(&mut self, k: &Q) -> Option<V>
where K: Borrow<Q> + Debug, Q: Ord + ?Sized, V: Debug
{

    let mut z = bst_search!(self.root, k);

    if z.is_none() {
        None
    }
    else {
        if left!(z).is_some() && right!(z).is_some() {
            let successor = bst_minimum!(right!(z));
            fake_swap!(z, successor);
            z = successor;
        }

        let p = paren!(z).upgrade();
        let z_dir = if p.is_some() { Some(index_of_child!(p, z)) } else { None };

        let child = child!(z, if left!(z).is_none() { Right } else { Left });
        subtree_shift!(self, z, child);

        if z.is_black() {
            if child.is_red() {
                color!(child, Black);
            }
            else if let Some(z_dir) = z_dir {
                self.fix_double_black(z_dir, p);
            }
        }

        Some(unwrap_into!(z).into_value())
    }
}

而处理这个双重黑节点就是删除重平衡要做的事情。

由上可得双黑节点不是根节点，并且由于删除前黑平衡的保证，它的邻居节点也不能是空节点，这样我们就有了一个讨论节点的关系的前提。

设双黑节点为 $\texttt{n}$ ，父节点为 $\texttt{p}$ ，邻居节点为 $\texttt{sib}$ ，邻居节点中与 $\texttt{n}$ 同向的孩子节点为 $\texttt{sib}_c$ ，反向的孩子节点为 $\texttt{sib}_d$ ，则所有的情况考虑的就是 $\texttt{p}$, $\texttt{sib}$ , $\texttt{sib}_c$ , $\texttt{sib}_d$ 这四个节点。

对 double black 的修复可以把这四个节点的颜色关系分为 $5$ 种情况，其中有三种是基础情况，剩下两种可以通过转换为基本情况来处理。

(case-1)

$\texttt{p}$, $\texttt{sib}$ , $\texttt{sib}_c$ , $\texttt{sib}_d$ 全是黑色：

$\texttt{sib}$ 反色为红，这样子树 $\texttt{n}$ 和 $\texttt{sib}$ 的黑高就都少了 $1$ ，于是虽然 $\texttt{p}$ 整体黑高少了 $\texttt{1}$ ，但至少在子树 $\texttt{p}$ 上重新达到了黑平衡，这样只需递归调用自身，一路向上修复即可（就像插入时修复红违背的 case-1 那样）。

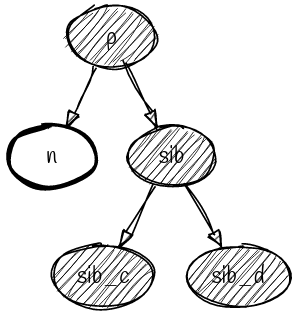
(case-2)

$\texttt{p}$是红色，$\texttt{sib}$ , $\texttt{sib}_c$ , $\texttt{sib}_d$ 全是黑色：

交换 $\texttt{p}$ 与 $\texttt{sib}$ 的颜色，这样 $\texttt{sib}$ 的黑高没有变化，而 $\texttt{sib}$ 的黑高增加了 $1$ ，这样双黑节点就直接解决了，这是一种完美的情况。

(case-3)

$\texttt{sib}$ 是黑色， $\texttt{sib}_d$ 是红色，（按照前述，此时 $\texttt{sib}_c$ 可以是红色或者黑色），$\texttt{p}$ 是任意颜色：

$\texttt{p}\leftrightarrow\texttt{sib}$ 旋转交换位置和颜色
$\texttt{sib}_d$ 颜色翻转为黑色

对于 $\texttt{n}$ ，增加了一个黑节点，黑高补全了；

对于子树 $\texttt{sib}_c$ 黑高保持不变，子树 $\texttt{sib}_d$ 路径上的黑节点少了一个 $\texttt{sib}$ 但自己从红变黑，黑高也是不变的，这样双黑节点也解决了，这是另一种完美情况。

[case-4]

$\texttt{sib}$ 是黑色， $\texttt{sib}_d$ 是黑色而且 $\texttt{sib}_c$ 是红色，$\texttt{p}$ 是任意颜色：

$\texttt{sib}\leftrightarrow\texttt{sib}_c$ 旋转交换位置和颜色

$\texttt{p}$ 的右子树的叶子节点的黑高不变（ $\texttt{sib}_c$ 两个孩子的叶子黑高不变，$\texttt{sib}_d$ 的叶子黑高不变）

这样情况就变成了 (case-3) （新 $\texttt{sib}$ 黑色，新 $\texttt{sib}_d$ 红色）的情况。

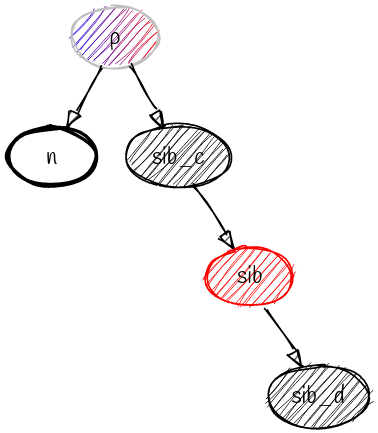
[case-5]

$\texttt{sib}$是红色（此时根据红黑约束条件，$\texttt{sib}_d$ ，$\texttt{sib}_c$ 必然是黑色）

$\texttt{p}\leftrightarrow\texttt{sib}$ 旋转交换位置和颜色

$\texttt{sib}_c$ 和 $\texttt{sib}_d$ 的黑高不变，$\texttt{n}$ 也还是双黑节点。

这时 $\texttt{sib}_c$ 变为新的 $\texttt{sib}$ 。然后根据新的 $\texttt{sib}$ 的子代的颜色进入 (case-2)，(case-3)， (case-4) 继续处理。

流程图

上述列举的情况虽然多且繁，有些复杂，但通过流程图还是能看得很清楚的。¹

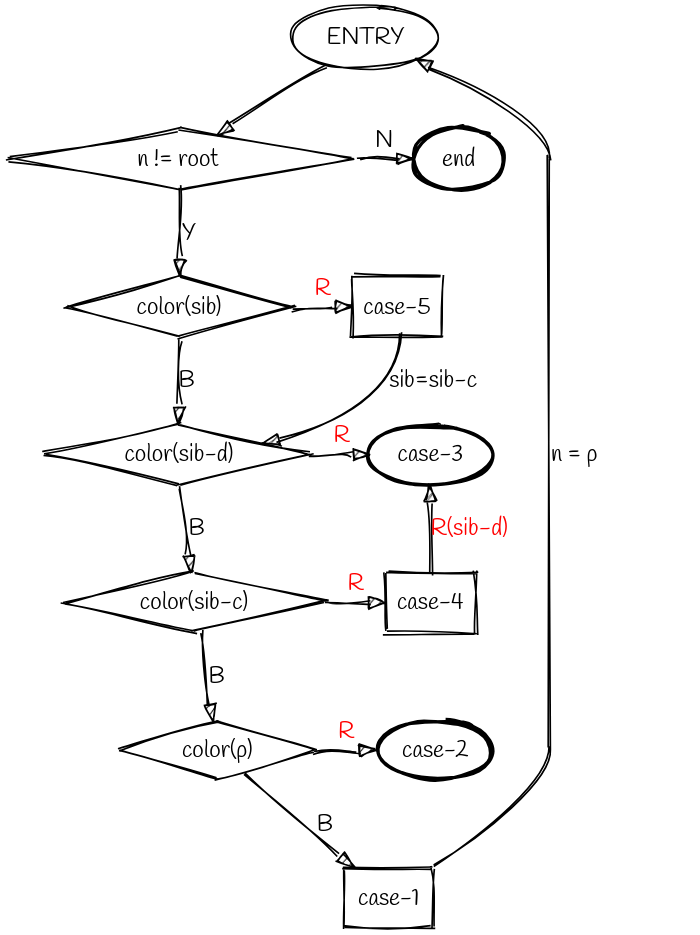
实现

// impl RB

/// Refer to my blog (BST(2) - RB(0) - 原始红黑树)
fn fix_double_black(&mut self, x_dir: Dir, p: Node<K, V>) {
    let sib_dir = x_dir.rev();
    let mut sib = child!(p, sib_dir);
    let mut sib_c = child!(sib, x_dir);
    let mut sib_d = child!(sib, sib_dir);

    /* case-5 */
    if sib.is_red() {
        rotate!(self, p, x_dir);

        sib = sib_c;
        sib_c = child!(sib, x_dir);
        sib_d = child!(sib, sib_dir);
    }

    macro_rules! case_3 {
        (p=$p:ident, x_dir=$x_dir:ident, sib_d=$sib_d:ident) => {
            rotate!(self, $p, $x_dir);
            $sib_d.color_flip();
        };
    }

    /* case-3 */
    if sib_d.is_red() {
        case_3!(p=p, x_dir=x_dir, sib_d=sib_d);
    }
    /* case-4 */
    else if sib_c.is_red() {
        rotate!(self, sib, sib_dir);
        case_3!(p=p, x_dir=x_dir, sib_d=sib);
    }
    /* case-2 */
    else if p.is_red() {
        swap!(node | p, sib, color);
    }
    /* case-1 */
    else {
        sib.color_flip();

        let pp = paren!(p).upgrade();

        if pp.is_some() {
            self.fix_double_black(index_of_child!(pp, p), pp);
        }
    }
}

// ...

哎呀我这代码写得太漂亮了，实在有必要自卖自夸一下：

结构清晰，教学模板！
最后的尾递归也实在漂亮，而且在现代编译器的优化里，递归调用通常还会快于手写的循环！

与之相比的是另一个业界广为流传的版本比如 OpenJDK TreeMap 实现，注释里可能暗示抄自 CLR (dot net runtime) ，但我强烈怀疑 CLR 也不是原创，毕竟红黑树是很早就有的概念。而不管原创是谁，这个版本显然看起来代码行数较少，但实在难以理解，它混合了一部分删除的代码并合并了case-2 。

一般地讲，代码一定要简单和易于理解，这通常比一时绝对的性能还要重要！因为简单就利于机器优化，易于理解就利于人工优化，这都利于算法的演进与必要条件下的特化。

像之前的对照版本，就是典型的传家宝，谁都不敢改，全是一模一样的代码然后在注释里写本代码抄自 xxx 。而我们的代码简单、易于理解，不管是调整流程还是省略几个宏重复的一些代码，都很容易。

注解

用 dot 画图的时候因为一个边指定 portPos后导致 dir 、arrowtail、arrowhead 属性设置都失效的问题，浪费一天时间，没解决，不知道这是什么特性还是 bug ，只能凑活一个图 ↩