BST(2) - RB(2) - AA树

Algorithm

January 20, 2023

基本概念

AA 树（以下简称 AA）由 Arne Andersson 在 1993 年发明提出。

AA 从理解到实现和 LLRB 是高度相似的（但是从作者关系上我们还是选择先介绍 LLRB），而一般的介绍资料，不管是 LLRB 还是 AA 的，都没有提这种密切的联系。

在 LLRB 里面，通过颜色关系，让节点与 2-3/2-4 树的节点一一对应；而在 AA 里每个节点也对应2-3树的节点。我们说 LLRB 是左偏的红黑树，那么 AA 实质上是比它（LLRB）出现更早的右偏红黑树（RLRB）。

基本性质

AA 节点有一个用于辅助树平衡的字段：$\texttt{level}$ ，表明节点所在的层级，叶子节点（这里的叶子不同于一般红黑树概念里的 $\texttt{nil}$ 叶子，而是普通意义上的叶子）的 $\texttt{level}$ 为 $1$ ， $\texttt{nil}$ 节点的 $\texttt{level}$ 为 $0$

如下就是一棵AA树：

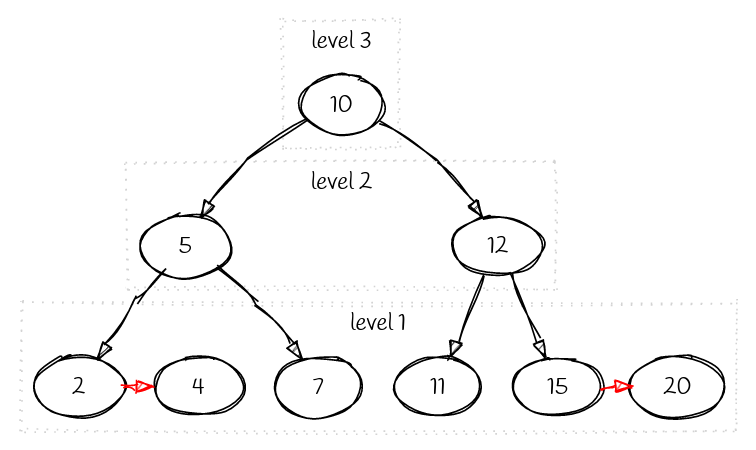
3-节点

在同一 $\texttt{level}$ 上相连的节点，对应的是 2-3树里的 3-节点

5特性

更具体地，AA 有以下 $5$ 个性质：

叶子节点（左右孩子都为 $\texttt{nil}$ 的节点）的 $\texttt{level}$ 为 $1$；
左孩子在下一层；
右孩子在同一层或下一层；
右孙子（右孩子的所有孩子）一定在下一层；
如果节点的 $\texttt{level} \gt 1$ ，它一定有两个孩子

解释一下这5个性质：

叶子节点 $\texttt{level} = 1$ ，是一个规定，设置 $\texttt{level}$ 的基准；
左节点在下一层因为这是 “LRRB“ ，只有右孩子能够在同一层；
“LRRB“ ，只有右孩子能够在同一层；
如果连续两个孩子都在同一层，那就出现了4-节点，而我们对应的 2-3 树，最多只能有 3-节点；
$\texttt{lv} \gt 1$ 的节点如果只有一个孩子，那么一定可以把它的孩子转到右边，并放在第一层

黑平衡

显然对于 AA 来说，叶子节点到祖先节点的左链接数应该保持相等，这就是它的黑平衡。

性质校验

impl_balance_validation!(AA ->
    #[cfg(test)]
    fn balance_validation(&self) {
        self.root.validate_balance();
    }
);


// impl AA

#[cfg(test)]
fn validate_balance(&self) {
    if self.is_none() { return }

    let left = left!(self);
    let right = right!(self);

    // Invariants-1: if x is leaf then x.lv == 1
    if left.is_none() && right.is_none() {
        assert_eq!(lv!(self), 1);
    }

    // Invariant-2.: x.left.lv + 1 = x.lv.
    assert_eq!(left.lv() + 1, self.lv());

    // Invariant-3.: x.right.lv == x.lv || x.right.lv + 1 == x.lv.
    assert!(
        right.lv() == self.lv()
        || right.lv() + 1 == self.lv()
    );

    // Invariant-4.: x.right.child.lv < x.lv
    if right.is_some() {
        assert!(left!(right).lv() < lv!(self));
        assert!(right!(right).lv() < lv!(self));
    }

    // Invariant-5.: if x.lv > 1 then x.children.len == 2
    if self.lv() > 1 {
        assert!(left.is_some() && right.is_some());
    }

    left.validate_balance();
    right.validate_balance();

}

// ...

基础定义

共同结构

impl_node!();
impl_node_!({ lv: usize });

impl_tree!(AA {});
impl_rotate_cleanup!(AA);


impl<K: Ord, V> AA <K, V> {

    pub fn new() -> Self {
        Self {
            root: Node::none()
        }
    }
	
    // ...
}


impl<K, V> Node<K, V> {

    fn lv(&self) -> usize {
        if self.is_none() {
            0
        }
        else {
            lv!(self)
        }
    }
    
    // ...
}

重平衡操作

为了维护插/删造成的树的性质的破坏（不平衡），发明了两种基本操作：（确保）（向右）倾斜（skew）、分离（4-节点）（split）

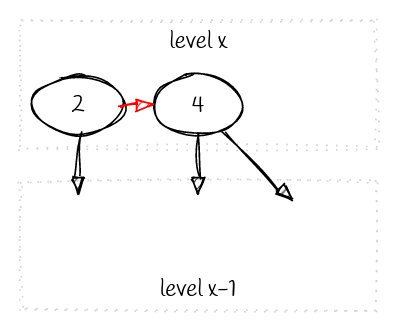
Skew

实际上是警戒哨的右旋，确保把箭头倾倒在右边

// impl 

fn skew(&mut self, mut t: Node<K, V>) -> Node<K, V> {
    debug_assert!(t.is_some());

    if left!(t).lv() == t.lv() {
        debug_assert!(left!(t).is_some());

        t = rotate!(self, t, Right)
    }

    t
}

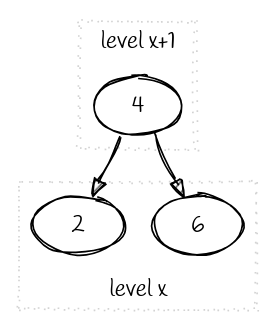
Split

实际是带警戒哨的左旋，确保把 4-节点 分割出来，另外不要忘了让新的根节点的 $\texttt{level} + 1$

// impl AA

fn split(&mut self, mut t: Node<K, V>) -> Node<K, V> {
    debug_assert!(t.is_some());

    let right = right!(t);

    if right.is_some() && right!(right).lv() == t.lv() {
        t = rotate!(self, t, Left);

        lv!(t, lv!(t) + 1);  // t == right
    }

    t
}

// ...

就像 LLRB 一样，插入删除的递归实现实际上是为了做重平衡

插入

严重依赖于子过程 insert_at 的递归操作，insert_at 返回旧的节点（如果存在）的值和新的根节点。

// impl AA

pub fn insert(&mut self, k: K, v: V) -> Option<V>
{
    let (root, popped) = self.insert_at(
        self.root.clone(),
        k,
        v
    );

    self.root = root;

    popped
}

fn insert_at(&mut self, mut t: Node<K, V>, k: K, v: V) -> (Node<K, V>, Option<V>) {
    if t.is_none() {
        return (node!(BST { k, v, lv: 1 }), None);
    }

    let popped;

    match k.cmp(key!(t)) {
        Equal => {  // replace node
            let old_valptr = attr!(t, val);
            attr!(t, val, boxptr!(v));

            return (t, Some(unboxptr!(old_valptr)));
        }
        Less => {
            let (left, popped_) = self.insert_at(left!(t), k, v);

            conn_left!(t, left);
            popped = popped_;
        }
        Greater => {
            let (right, popped_) = self.insert_at(right!(t), k, v);

            conn_right!(t, right);
            popped = popped_;
        }
    }

    t = self.skew(t);
    t = self.split(t);

    (t, popped)
}

// ...

删除

严重依赖于子过程 remove_at 的递归操作，remove_at 返回符合删除条件的节点（用指针表示）的值和新的根节点。

如果被删除的节点不是叶子节点，就在它不为空的孩子上寻找后继或前驱，然后在那个孩子上使用原递归调用删除，最后用假替换把删除后的前驱或后继节点的 key-val 与当前节点交换，并进行对该节点的重平衡操作。

每次递归调用过程的重平衡操作可以总结为 $3$ 次分别在 t、t.right、t.right.right 上 skew 和 $2$ 次在 t 和 t.right 上 split 。注意得是每次 skew 或 split，不仅根节点变动，右孩子的节点也会变动，需要动态计算。

// impl AA

pub fn remove<Q>(&mut self, k: &Q) -> Option<V>
where K: Borrow<Q> + Debug, Q: Ord + ?Sized, V: Debug
{
    let (root, popped) = self.remove_at(self.root.clone(), k);

    self.root = root;

    popped.map(|(k_ptr, v_ptr)| {
        unboxptr!(k_ptr);
        unboxptr!(v_ptr)
    })
}    


fn remove_at<Q>(&mut self, mut t: Node<K, V>, k: &Q)
-> (Node<K, V>, Option<(*mut K, *mut V)>)
where K: Borrow<Q> + Debug, Q: Ord + ?Sized, V: Debug
{
    if t.is_none() {
        return (t, None);
    }

    let popped =

    match k.cmp(key!(t).borrow()) {
        Less => {
            let (left, popped_)
            = self.remove_at(left!(t), k);
            conn_left!(t, left);
            popped_
        }
        Greater => {
            let (right, popped_)
            = self.remove_at(right!(t), k);
            conn_right!(t, right);
            popped_
        }
        Equal => {
            if left!(t).is_none() && right!(t).is_none() {
                let old_keyptr = attr!(t, key);
                let old_valptr = attr!(t, val);

                attr!(t, key, null_mut());
                attr!(t, val, null_mut());

                return (
                    Node::none(),
                    Some((
                        old_keyptr,
                        old_valptr
                    ))
                );
            }

            let nil_dir = if left!(t).is_none() { Left } else { Right };
            let l = if nil_dir.is_left()
            { bst_successor!(t) } else { bst_predecessor!(t) };

            let (child, l_entry)
            = self.remove_at(child!(t, nil_dir.rev()), key!(l).borrow());

            conn_child!(t, child, nil_dir.rev());

            let old_keyptr = attr!(t, key);
            let old_valptr = attr!(t, val);

            let (k, v) = l_entry.unwrap();
            attr!(t, key, k);
            attr!(t, val, v);

            Some((old_keyptr, old_valptr))
        }
    };

    if left!(t).lv() + 1 < t.lv() || right!(t).lv() + 1 < t.lv() {
        /* Decrease lv */

        let left = left!(t);
        let right = right!(t);

        let lv = std::cmp::min(left.lv(), right.lv()) + 1;

        if lv < t.lv() {
            lv!(t, lv);

            if lv < right.lv() {
                lv!(right, lv);
            }
        }

        /* Tripple skew */

        t = self.skew(t);

        // Warnning: right(t) changes after this
        self.skew(right!(t));

        if right!(t).is_some() && right!(right!(t)).is_some() {
            self.skew(right!(right!(t)));
        }

        /* Double split */

        t = self.split(t);

        self.split(right!(t));
    }

    (t, popped)
}

// ...

总结

AA 是更扁平化的红黑树变种也因此需要付出更多的旋转来维护平衡，实际测试感觉和 AVL 差不多，总体结果就是没什么用，一方面不如 AVL 更容易实现，一方面也丢掉了红黑树维护旋转少的特点，和 LLRB 一样鸡肋。